infoGAN Review

0. Abstract

GAN의 정보이론을 활용하는 쪽으로 확장한 InfoGAN은 완전한 un-supervised learning 방식으로 disentangled representation을 학습할 수 있습니다. 이를 위해 본 논문에서는 latent variable과 observation간에 mutual information(상호정보)을 공식화하여 목적함수에 추가하였고, 이 mutual information(상호정보)를 최대화하는 방향으로 generator가 학습되게 하였습니다.

1. Introduction

비지도 학습은 풍부한 양의 unlabelled data로부터 가치를 추출하는 일반적인 문제로 묘사될 수 있습니다. representation learning(표현 학습)은 대표적인 비지도학습의 프레임워크로 unlabeled 데이터로부터 중요한 의미론적 특징을 쉽게 해독할 수 있는 인자들을 나타내는 representation을 학습하는 것을 목표로 합니다.

비지도 학습의 표현학습을 통해 data instance들의 핵심적인 특징을 명식적으로 나타내는 disentangleed representation을 학습할 수 있다면, 이것은 classfication 등의 dawnstream task에 유용하게 사용될 수 있습니다.

비지도 학습 연구분야의 대부분은 생성 모델링(generative modeling)이 주도하고 있습니다. 생성 모델링에서는 관측된 데이터를 합성하거나 창조하는 생성모델의 능력이 데이터에 대한 깊은 이해를 동반한다고 생각하며, 좋은 생성모델은 훈련과정에서 따로 명시하지 않더라도 스스로 disentangled representation을 학습할 것이라 생각됩니다.

본 논문에서는 2 가지의 기여점을 중심으로 서술되었습니다.

• GAN의 generator에 input되는 noise 변수들의 어떤 고정된 부분집합(latent code)와 관측 데이터간에 mutual information을 최대화하게 함으로써 해석가능하며 풍부한 의미를 갖는 representation을 학습할 수 있게끔 목적함수를 수정
• mutual information을 cost로 사용하는 생성모델링이 disentangled representation learning에 대한 좋은 접슨법이 될 수 있음을 의미

요약 및 핵심

→ 기본적인 idea : 기존의 GAN은 생성모델의 input이 $$z$$ 하나 인 것에 비해 infoGAN은 $$(z,c)$$로 input에 code라는 latent variable $$c$$가 추가되고, GAN objective에 add-on을 추가해 Generator가 학습을 할 때, latent 공간($z$-space)에서 추가로 넣어준 $$c$$와 생성된 샘플 사이의 mutual information이 높아지도록 도와줍니다.

2. Mutual Information for Indicing Latent Codes

기존의 GAN의 Generator는 간단한 1D continuous latent vector $$z$$를 사전에 가정한 prior로부터 샘플링하여 그대로 사용합니다. 저자들은 이런 방식으로 $$z$$를 사용할 경우, generator의 $$z$$의 각 차원마다 분리된 개별적인 semantic feature를 학습하는게 아니라 차원들이 서로 복잡하게 얽힌 표현이 학습된다고 주장합니다.

그러나 실제로 많은 도메인의 데이터들은 자연스럽게 서로 잘 분리되어있는 의미론적 변동인자를 내재하고 있습니다.

MNIST를 예로 들자면,
숫자 종류(0~9)에 대한 변동을 포착하는 discrete latent variable, 숫자의 각도나 기울기 변동을 포착하는 continuous latent variable, 숫자의 두께 변동을 포착하는 continuous latent variable 등 서로 독립적인 세 가지의 변동인자를 각각 따로따로 학습 할 수 있으면 이상적인 결과를 나타낼 수 있습니다.

논문에서는 기존의 GAN처럼 single noise vector를 사용하지 않고, noise vector를 다음의 두 part로 분류하여 사용합니다.

1. $$z$$ : indissoluble noise vector(분해 불가능한 노이즈 벡터)
2. $$c$$ : 데이터 분포의 핵심적인 의미론적 특징에 대응 되는 latent code → $$c = [c_1,c_2,…,c_L]$$

방법

• Generator에 $z$와 $c$가 함께 input으로 포함됩니다. → $$G(z,c)$$
• 목적함수에 정보이론적 규제 term $$I(c;G(z,c))$$를 추가합니다.
  여기서 $$I(c;G(z,c))$는 latent code $$c$와 Generator의 distribution $G(z,c)$간에 상호정보를 의미합니다.

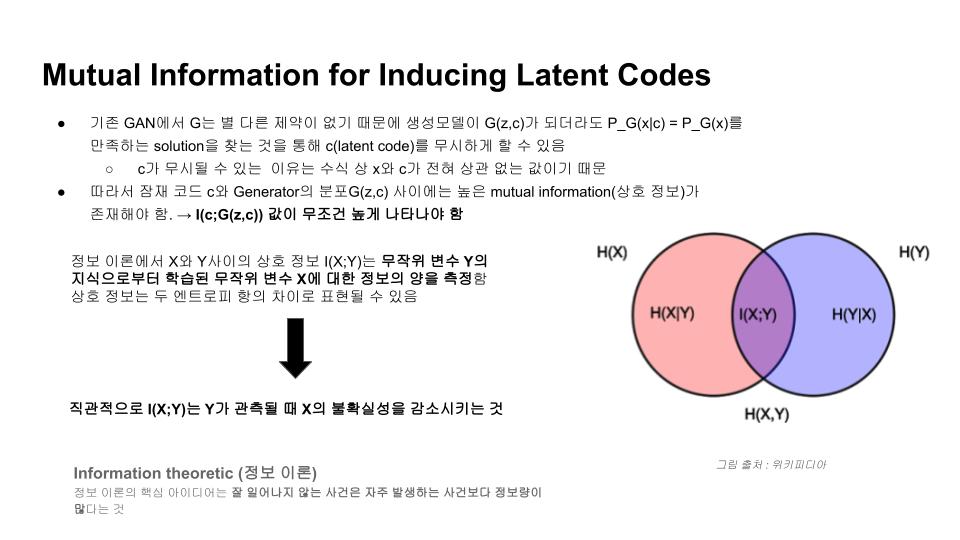
정보 이론에서 두 변수 X,Y 간에 상호정보 $$I(X;Y)$$는 다음과 같이 표현됩니다.

이것을 둘 중 하나의 변수로 관측함으로써 감소하는 나머지 변수에 대한 불확실성의 크기를 계량하는 측도로 볼 수 있습니다. 두 변수가 독립적이라면 상호정보는 $$0$$이 되고, 두 변수가 가역함수의 관계일 때 최대가 됩니다.
즉, 우리는 어떤 임의의 $$x ~ G(z,c)$$에 대해 $$P(c|x)$$가 작은 entropy를 갖는 것을 원하게 됩니다. 같은 말로 우리는 $$I(c;G(z,c))$$가 최대화 되는 방향으로 $$G(.)$$가 학습되길 원합니다.

이를 반영하는 새로운 목적함수는 다음과 같습니다.

요약 및 핵심

그림에서와 같이 basis의 방향인 x축 혹은 y축으로 움직일 때 마다 규칙성이 존재하지 않고 무작위로 색이 변동되는 것을 확인할 수 있습니다. 색을 데이터에서의 어떤 의미라고 가정했을 때 이런 representation space에서 유의미한 코드를 찾기는 어려워지게 됩니다.

하지만 아래와 같이 representation space를 학습할 수 있다면 이전과 달리 각각의 basis demension이 의미를 가지고 이를 해석하기가 편리해집니다.

이렇게 representation을 학습할 때, 좀 더 좋은 성질을 갖도록 제약을 줄 수 있다면 훨씬 학습이 용이할 것이라는 것이 InfoGAN의 저자들이 말하고자 하는 바 입니다.

3. Variational Mutual Information Maximization

문제는 $I(c;G(z,c))$는 우리가 알지못하는 $c$에대한 true posterior $P(c|x)$에 대한 계산을 요구하므로 직접 최적화하는것이 어렵습니다. 대신에 VAE와 같이 $P(c|x)$를 근사하는 단순한 보조분포 $Q(c|x)$를 활용하여 상호정보에 대한 Variational Lower Bound를 구해서 간접적으로 최적화를 진행할 수 있습니다.

상호정보의 하한을 구하는 이 테크닉은 Variational Information Maximization이라고 알려져 있습니다.
이 식에서 latent code의 엔트로피인 $H(c)$는 $c$에 대해 흔한 분포를 가정할 경우, analytical한 form으로 쉽게 계산될 수 있지만, 본 논문에서는 $c$의 분포를 고정한 채 사용하여 $H(c)$를 상수로 취급하고 좌측의 항만 최적화했다고 소개하고 있습니다.

→ $I(c;G(z,c))$를 최대화 하는 대신 그것의 하한인 $L_I(G,Q)$를 최대화 하는 방식입니다. 그런데 식에서는 $c^＇∼P(c|x)$와 같이 $c$의 true posterior로부터 샘플에 대한 기댓값을 구하는 파트가 존재함을 확인할 수 있습니다. 이것은

위 식을 이용하여 아래의 식의 첫번째 line을 쓸 수 있고, 우리가 모르는 True posterior 대신 흔한 분포로 가정할 수 있는 $c$의 marginal distribution $P(c)$를 사용함으로써 문제를 해결할 수 있습니다.

$L_I(G,Q)$에서 $Q$는 직접적으로 최대화될 수 있고, $G$는 reparametrization trick을 사용하여 최대화될 수 있기 때문에, 기존 GAN의 train 프로세스에 변경없이 Objective에 추가될 수 있습니다.

이렇게 유도되는 알고리즘을 Information Maximizing Generative Adversarial Networks(InfoGAN) 이라 부르며, 그것의 목적함수는 다음과 같습니다.

4. Implementation

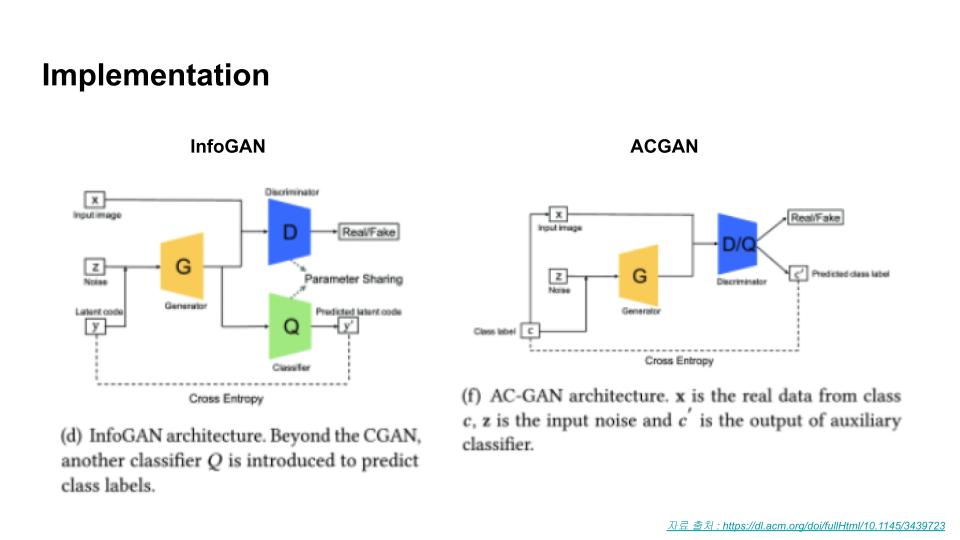
상호정보를 간접적으로 최적화하기 위해 보조 분포로써 도입한 $Q(c|x)$는 head부분을 제외한 나머지 모든 layer를 공유하게 구현했습니다. 따라서 $c$의 조건부 분포에 대한 출력을 얻게끔 하는 FC layer 하나만 추가하면 되기 때문에 추가되는 파라미터는 매우 적습니다.

→ Objective에 추가된 $L_I(G,Q)$ term을 계산하기 위해 $Q(c|x)$를 출력하는 head를 별도로 추가함 일반적인 GAN보다 목적함수의 수렴이 대부분 빠르고, 새로 추가되는 상호정보항 반영비율에 대한 하이퍼파라미터 $λ$는 튜닝이 간단하다고 합니다.

5. Experiments

5.1 Mutual Information Maximization

latent code $c$와 generator images $G(z,c)$간에 상호정보가 제안한 방법대로 최대화 되었는지 확인하는 실험입니다.

그림과 같이 목적함수에 $L_I(G,Q)$ term이 추가된 InfoGAN은 몇번의 에폭을 진행함에 따라 상호정보 하한이 잘 최대화된 것을 확인할 수 있습니다.
비교를 위해 동일한 네트워크 구조이지만 목적함수 $L_I(G,Q)$ term이 추가되지 않은 baseline모델을 training한 결과, 상호 정보의 하한인 $L_I(G,Q)$값이 0에 가까워지는(latent code와 생성되는 이미지간의 연관성이 없는) 방향으로 학습되는 것을 확인할 수 있습니다.

5.2 Disentangled Representation

아래는 3D face 데이터에서 학습한 결과입니다.

얼굴 각도나 시선의 고도 뿐만 아니라 음영이 지는 각도 등에 대해서도 잘 나타내어집니다.

3D face 데이터와 마찬가지로 얼굴의 포즈를 학습하기도 했지만 안경의 유무나 헤어스타일, 감정 등의 변동 인자들이 잘 학습됨을 확인할 수 있습니다.

6. Conclusion & Future works

1. Information Maximizing 방식을 도입한 GAN을 InfoGAN이라는 표현학습 알고리즘으로 제안했습니다.
   • 복잡한 데이터셋(celeba 등)에 대해서도 해석력이 좋으며 disentangled된 representation을 얻을 수 있었습니다.
   • 훈련이 쉽다는 장점과 계산 cost가 일반 GAN과 비교하더라도 거의 차이가 없습니다.
2. 상호정보(mutual information)을 representation의 추출에 사용하자가 이 논문에서의 핵심이고 이 아이디어는 VAE와 같은 다른 생성모델에도 확장될 수 있습니다.

학습목표

 이번 강의에서는 고유값 분해와 밀접한 관련을 가지는 대각화의 개념에 대해 배워보겠습니다. 이는 나중에 배울 특이값 분해(SVD, Singular Value Decomposition)와도 밀접한 관련이 있으니 숙지하고 넘어가시길 바랍니다.

핵심 키워드

• 대각화행렬(Diagonalizable Matrix)

학습하기

 이제 대각화(Diagonalize)를 생각해보죠. 기본적으로 이건 정방행렬에 대해 생각하는 개념이구요. Diagonal matrix라는, (i,i)의 값만 존재하고 나머지 좌표의 값은 0인 그런 행렬로 변환하는 과정을 대각화라고 생각하시면 됩니다. 다만 이건 모든 행렬에 대해 가능한게 아니라, 되는 행렬이 있고, 안되는 행렬이 있습니다. 아래 식에 등장하는 V matrix를 찾을 수 있는가 없는가로 구분할 수 있겠습니다. 이렇게, 대각화가 가능한 행렬을 Diagonalizable matrix라고 부릅니다.

 그럼 이러한 Diagonal matrix를 어떻게 찾을 것인가. 아래 수식의 두 번째를 잘 보셔야합니다. 좌측에서 우측은 갈 수 있찌만, 우측에서 좌측은 불가능합니다. V라는 행렬이 역행렬이 존재할 때는 우측에서 좌측이 가능하겠죠.

 AV와 VD를 각각 생각해봅시다. AV에서 V라는건, n개의 컬럼을 가지니까, 아래와 같이 연산할 수 있겠죠. 그리고 VD도 마찬가지로 아래와 같이 연산될겁니다. 그러면 이제, AV=VD라는 식에서, Av1=r1v1, Av2=r2v2, ... 라는 등식을 얻어낼 수 있겠죠.

 그렇게 정리된 각각의 식이, 생각해보면 고유벡터에 해당하는 식과 정확히 동일합니다. 고유값 r1,r2,...,rn에 대한 고유벡터 v1,v2,..,vn이 된 셈이죠. 그런 관점에서 보면 V가 역행렬을 갖기 위해서는, 정방행렬이 되어야하고, 즉슨 n개의 고유벡터들이 반드시 선형독립이어야겠죠. 

 따라서 아래의 그림과 같이, V는 반드시 정방행렬이어야하고, n개의 선형독립 컬럼을 가져야합니다. V는 고유벡터의 컬럼이었기 때문에, (A-rI)x=0를 생각해볼 때, A matrix가 반드시 n개의 선형독립 고유벡터를 지녀야만합니다. 그렇지 않다면, Diagonalizable하지 않게 되는 것이겠죠. 이상입니다.