infoGAN Review

0. Abstract

GAN의 정보이론을 활용하는 쪽으로 확장한 InfoGAN은 완전한 un-supervised learning 방식으로 disentangled representation을 학습할 수 있습니다. 이를 위해 본 논문에서는 latent variable과 observation간에 mutual information(상호정보)을 공식화하여 목적함수에 추가하였고, 이 mutual information(상호정보)를 최대화하는 방향으로 generator가 학습되게 하였습니다.

1. Introduction

비지도 학습은 풍부한 양의 unlabelled data로부터 가치를 추출하는 일반적인 문제로 묘사될 수 있습니다. representation learning(표현 학습)은 대표적인 비지도학습의 프레임워크로 unlabeled 데이터로부터 중요한 의미론적 특징을 쉽게 해독할 수 있는 인자들을 나타내는 representation을 학습하는 것을 목표로 합니다.

비지도 학습의 표현학습을 통해 data instance들의 핵심적인 특징을 명식적으로 나타내는 disentangleed representation을 학습할 수 있다면, 이것은 classfication 등의 dawnstream task에 유용하게 사용될 수 있습니다.

비지도 학습 연구분야의 대부분은 생성 모델링(generative modeling)이 주도하고 있습니다. 생성 모델링에서는 관측된 데이터를 합성하거나 창조하는 생성모델의 능력이 데이터에 대한 깊은 이해를 동반한다고 생각하며, 좋은 생성모델은 훈련과정에서 따로 명시하지 않더라도 스스로 disentangled representation을 학습할 것이라 생각됩니다.

본 논문에서는 2 가지의 기여점을 중심으로 서술되었습니다.

• GAN의 generator에 input되는 noise 변수들의 어떤 고정된 부분집합(latent code)와 관측 데이터간에 mutual information을 최대화하게 함으로써 해석가능하며 풍부한 의미를 갖는 representation을 학습할 수 있게끔 목적함수를 수정
• mutual information을 cost로 사용하는 생성모델링이 disentangled representation learning에 대한 좋은 접슨법이 될 수 있음을 의미

요약 및 핵심

→ 기본적인 idea : 기존의 GAN은 생성모델의 input이 $$z$$ 하나 인 것에 비해 infoGAN은 $$(z,c)$$로 input에 code라는 latent variable $$c$$가 추가되고, GAN objective에 add-on을 추가해 Generator가 학습을 할 때, latent 공간($z$-space)에서 추가로 넣어준 $$c$$와 생성된 샘플 사이의 mutual information이 높아지도록 도와줍니다.

2. Mutual Information for Indicing Latent Codes

기존의 GAN의 Generator는 간단한 1D continuous latent vector $$z$$를 사전에 가정한 prior로부터 샘플링하여 그대로 사용합니다. 저자들은 이런 방식으로 $$z$$를 사용할 경우, generator의 $$z$$의 각 차원마다 분리된 개별적인 semantic feature를 학습하는게 아니라 차원들이 서로 복잡하게 얽힌 표현이 학습된다고 주장합니다.

그러나 실제로 많은 도메인의 데이터들은 자연스럽게 서로 잘 분리되어있는 의미론적 변동인자를 내재하고 있습니다.

MNIST를 예로 들자면,
숫자 종류(0~9)에 대한 변동을 포착하는 discrete latent variable, 숫자의 각도나 기울기 변동을 포착하는 continuous latent variable, 숫자의 두께 변동을 포착하는 continuous latent variable 등 서로 독립적인 세 가지의 변동인자를 각각 따로따로 학습 할 수 있으면 이상적인 결과를 나타낼 수 있습니다.

논문에서는 기존의 GAN처럼 single noise vector를 사용하지 않고, noise vector를 다음의 두 part로 분류하여 사용합니다.

1. $$z$$ : indissoluble noise vector(분해 불가능한 노이즈 벡터)
2. $$c$$ : 데이터 분포의 핵심적인 의미론적 특징에 대응 되는 latent code → $$c = [c_1,c_2,…,c_L]$$

방법

• Generator에 $z$와 $c$가 함께 input으로 포함됩니다. → $$G(z,c)$$
• 목적함수에 정보이론적 규제 term $$I(c;G(z,c))$$를 추가합니다.
  여기서 $$I(c;G(z,c))$는 latent code $$c$와 Generator의 distribution $G(z,c)$간에 상호정보를 의미합니다.

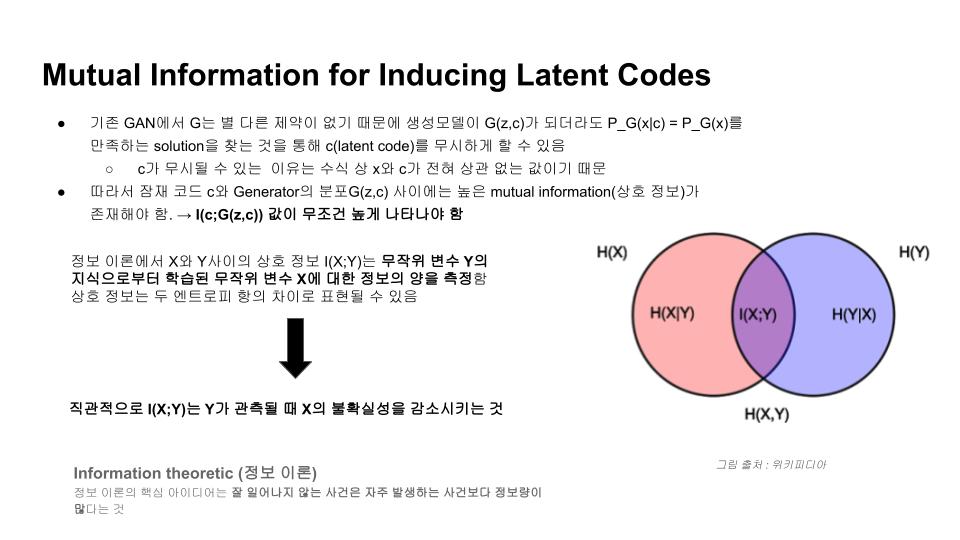
정보 이론에서 두 변수 X,Y 간에 상호정보 $$I(X;Y)$$는 다음과 같이 표현됩니다.

이것을 둘 중 하나의 변수로 관측함으로써 감소하는 나머지 변수에 대한 불확실성의 크기를 계량하는 측도로 볼 수 있습니다. 두 변수가 독립적이라면 상호정보는 $$0$$이 되고, 두 변수가 가역함수의 관계일 때 최대가 됩니다.
즉, 우리는 어떤 임의의 $$x ~ G(z,c)$$에 대해 $$P(c|x)$$가 작은 entropy를 갖는 것을 원하게 됩니다. 같은 말로 우리는 $$I(c;G(z,c))$$가 최대화 되는 방향으로 $$G(.)$$가 학습되길 원합니다.

이를 반영하는 새로운 목적함수는 다음과 같습니다.

요약 및 핵심

그림에서와 같이 basis의 방향인 x축 혹은 y축으로 움직일 때 마다 규칙성이 존재하지 않고 무작위로 색이 변동되는 것을 확인할 수 있습니다. 색을 데이터에서의 어떤 의미라고 가정했을 때 이런 representation space에서 유의미한 코드를 찾기는 어려워지게 됩니다.

하지만 아래와 같이 representation space를 학습할 수 있다면 이전과 달리 각각의 basis demension이 의미를 가지고 이를 해석하기가 편리해집니다.

이렇게 representation을 학습할 때, 좀 더 좋은 성질을 갖도록 제약을 줄 수 있다면 훨씬 학습이 용이할 것이라는 것이 InfoGAN의 저자들이 말하고자 하는 바 입니다.

3. Variational Mutual Information Maximization

문제는 $I(c;G(z,c))$는 우리가 알지못하는 $c$에대한 true posterior $P(c|x)$에 대한 계산을 요구하므로 직접 최적화하는것이 어렵습니다. 대신에 VAE와 같이 $P(c|x)$를 근사하는 단순한 보조분포 $Q(c|x)$를 활용하여 상호정보에 대한 Variational Lower Bound를 구해서 간접적으로 최적화를 진행할 수 있습니다.

상호정보의 하한을 구하는 이 테크닉은 Variational Information Maximization이라고 알려져 있습니다.
이 식에서 latent code의 엔트로피인 $H(c)$는 $c$에 대해 흔한 분포를 가정할 경우, analytical한 form으로 쉽게 계산될 수 있지만, 본 논문에서는 $c$의 분포를 고정한 채 사용하여 $H(c)$를 상수로 취급하고 좌측의 항만 최적화했다고 소개하고 있습니다.

→ $I(c;G(z,c))$를 최대화 하는 대신 그것의 하한인 $L_I(G,Q)$를 최대화 하는 방식입니다. 그런데 식에서는 $c^＇∼P(c|x)$와 같이 $c$의 true posterior로부터 샘플에 대한 기댓값을 구하는 파트가 존재함을 확인할 수 있습니다. 이것은

위 식을 이용하여 아래의 식의 첫번째 line을 쓸 수 있고, 우리가 모르는 True posterior 대신 흔한 분포로 가정할 수 있는 $c$의 marginal distribution $P(c)$를 사용함으로써 문제를 해결할 수 있습니다.

$L_I(G,Q)$에서 $Q$는 직접적으로 최대화될 수 있고, $G$는 reparametrization trick을 사용하여 최대화될 수 있기 때문에, 기존 GAN의 train 프로세스에 변경없이 Objective에 추가될 수 있습니다.

이렇게 유도되는 알고리즘을 Information Maximizing Generative Adversarial Networks(InfoGAN) 이라 부르며, 그것의 목적함수는 다음과 같습니다.

4. Implementation

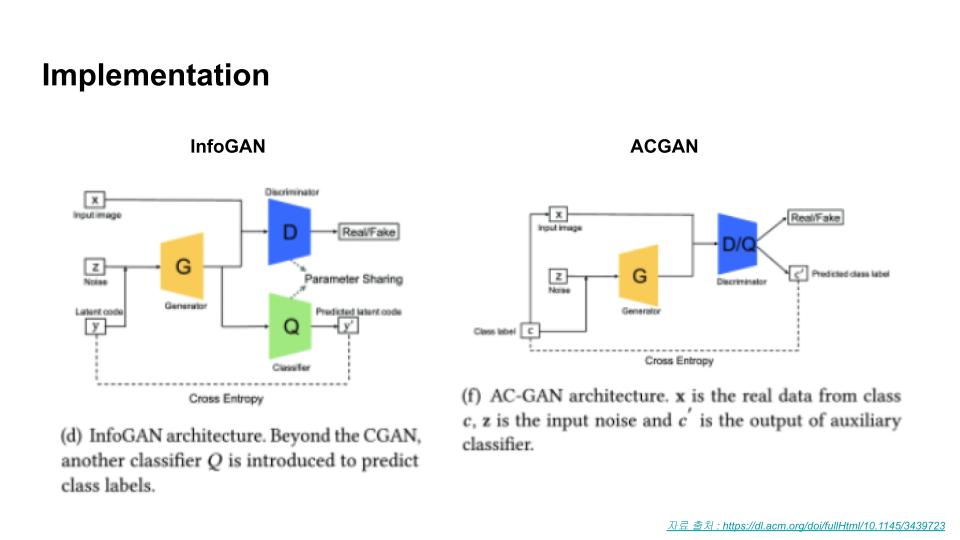
상호정보를 간접적으로 최적화하기 위해 보조 분포로써 도입한 $Q(c|x)$는 head부분을 제외한 나머지 모든 layer를 공유하게 구현했습니다. 따라서 $c$의 조건부 분포에 대한 출력을 얻게끔 하는 FC layer 하나만 추가하면 되기 때문에 추가되는 파라미터는 매우 적습니다.

→ Objective에 추가된 $L_I(G,Q)$ term을 계산하기 위해 $Q(c|x)$를 출력하는 head를 별도로 추가함 일반적인 GAN보다 목적함수의 수렴이 대부분 빠르고, 새로 추가되는 상호정보항 반영비율에 대한 하이퍼파라미터 $λ$는 튜닝이 간단하다고 합니다.

5. Experiments

5.1 Mutual Information Maximization

latent code $c$와 generator images $G(z,c)$간에 상호정보가 제안한 방법대로 최대화 되었는지 확인하는 실험입니다.

그림과 같이 목적함수에 $L_I(G,Q)$ term이 추가된 InfoGAN은 몇번의 에폭을 진행함에 따라 상호정보 하한이 잘 최대화된 것을 확인할 수 있습니다.
비교를 위해 동일한 네트워크 구조이지만 목적함수 $L_I(G,Q)$ term이 추가되지 않은 baseline모델을 training한 결과, 상호 정보의 하한인 $L_I(G,Q)$값이 0에 가까워지는(latent code와 생성되는 이미지간의 연관성이 없는) 방향으로 학습되는 것을 확인할 수 있습니다.

5.2 Disentangled Representation

아래는 3D face 데이터에서 학습한 결과입니다.

얼굴 각도나 시선의 고도 뿐만 아니라 음영이 지는 각도 등에 대해서도 잘 나타내어집니다.

3D face 데이터와 마찬가지로 얼굴의 포즈를 학습하기도 했지만 안경의 유무나 헤어스타일, 감정 등의 변동 인자들이 잘 학습됨을 확인할 수 있습니다.

6. Conclusion & Future works

1. Information Maximizing 방식을 도입한 GAN을 InfoGAN이라는 표현학습 알고리즘으로 제안했습니다.
   • 복잡한 데이터셋(celeba 등)에 대해서도 해석력이 좋으며 disentangled된 representation을 얻을 수 있었습니다.
   • 훈련이 쉽다는 장점과 계산 cost가 일반 GAN과 비교하더라도 거의 차이가 없습니다.
2. 상호정보(mutual information)을 representation의 추출에 사용하자가 이 논문에서의 핵심이고 이 아이디어는 VAE와 같은 다른 생성모델에도 확장될 수 있습니다.

학습목표

 이번 강의에서는 고유값 분해와 밀접한 관련을 가지는 대각화의 개념에 대해 배워보겠습니다. 이는 나중에 배울 특이값 분해(SVD, Singular Value Decomposition)와도 밀접한 관련이 있으니 숙지하고 넘어가시길 바랍니다.

핵심 키워드

• 대각화행렬(Diagonalizable Matrix)

학습하기

 이제 대각화(Diagonalize)를 생각해보죠. 기본적으로 이건 정방행렬에 대해 생각하는 개념이구요. Diagonal matrix라는, (i,i)의 값만 존재하고 나머지 좌표의 값은 0인 그런 행렬로 변환하는 과정을 대각화라고 생각하시면 됩니다. 다만 이건 모든 행렬에 대해 가능한게 아니라, 되는 행렬이 있고, 안되는 행렬이 있습니다. 아래 식에 등장하는 V matrix를 찾을 수 있는가 없는가로 구분할 수 있겠습니다. 이렇게, 대각화가 가능한 행렬을 Diagonalizable matrix라고 부릅니다.

 그럼 이러한 Diagonal matrix를 어떻게 찾을 것인가. 아래 수식의 두 번째를 잘 보셔야합니다. 좌측에서 우측은 갈 수 있찌만, 우측에서 좌측은 불가능합니다. V라는 행렬이 역행렬이 존재할 때는 우측에서 좌측이 가능하겠죠.

 AV와 VD를 각각 생각해봅시다. AV에서 V라는건, n개의 컬럼을 가지니까, 아래와 같이 연산할 수 있겠죠. 그리고 VD도 마찬가지로 아래와 같이 연산될겁니다. 그러면 이제, AV=VD라는 식에서, Av1=r1v1, Av2=r2v2, ... 라는 등식을 얻어낼 수 있겠죠.

 그렇게 정리된 각각의 식이, 생각해보면 고유벡터에 해당하는 식과 정확히 동일합니다. 고유값 r1,r2,...,rn에 대한 고유벡터 v1,v2,..,vn이 된 셈이죠. 그런 관점에서 보면 V가 역행렬을 갖기 위해서는, 정방행렬이 되어야하고, 즉슨 n개의 고유벡터들이 반드시 선형독립이어야겠죠. 

 따라서 아래의 그림과 같이, V는 반드시 정방행렬이어야하고, n개의 선형독립 컬럼을 가져야합니다. V는 고유벡터의 컬럼이었기 때문에, (A-rI)x=0를 생각해볼 때, A matrix가 반드시 n개의 선형독립 고유벡터를 지녀야만합니다. 그렇지 않다면, Diagonalizable하지 않게 되는 것이겠죠. 이상입니다.

학습목표

 이번 시간에는 지난 시간에 배운 새로운 벡터 공간의 개념을 바탕으로 고유벡터와 고유값을 더 깊이 이해하고 특성방정식(Charateristic Equation)을 통해 이들을 구하는 법을 알아보겠습니다.

핵심 키워드

• 특성방정식(Characteristic Equation)

학습하기

 자 앞서 영공간에 대해 살펴봤는데, 다시 고유벡터로 돌아와봅시다. 고유벡터와 고유값을 구하기 위한 식이 아래와 같은 식이고, A-rI를 B로 치환하면 이는 결국 Bx=0라는 식의 솔루션, 즉 Nul B가 되는 셈입니다. 그리고 이러한 공간을, Eigenspace라고 하죠. 앞서 봤던 Rank-Nullity thm의 내용을 그대로 쓸 수 있겠죠. A-rI가 3차원일 때, A-rI가 2개의 기저벡터를 갖는다면, 고유벡터는 1차원을 갖는다. 이런 식의 접근이 가능하다는 말입니다.

 이러한 내용을 안 지금, 다시 한번 아래의 예제를 봅시다. Row A에서 선형독립인 벡터가 1개입니다. 그럼 고유벡터는 몇 개가 될 수 있을까요. 반드시 1개겠죠. dim(Row A) + dim(Nul A) = 2이 나와야하니까요.

 그리고, 이 예제에서는 -3이라는 고유값도 갖는데, 이 경우에도 Row A의 선형독립 벡터는 1개이며, 고유벡터도 1개 밖에 존재할 수 없습니다. 아니 정확하게는 고유벡터의 개수가 아니라 선형독립인 벡터의 개수가 1개인거죠.

 이번에는 저런 고유값을 어떻게 찾느냐-에 대해 말해봅시다. 앞의 예제를 떠올려보면, A-rI를 선형의존하게끔 만들어줬을 때, 고유벡터를 찾을 수 있었습니다. 선형의존하다는 말은 해당 행렬이 역행렬을 갖지 못한다는 말이기도 했죠. 물론 역행렬을 갖고 말고 하는 문제는, 정방행렬에서만 생각하셔야합니다. 그럼 역행렬을 갖지 못한다는 말은 det(A-rI)=0라는 말이기도 했죠. 때문에 저희는 det(A-rI)=0를 만족하는 r를 찾으면, 이게 고유값이 될 것을 알 수 있습니다. 그리고 이게 바로 특정방정식(Characteristic Equation)입니다.

 예제를 봅시다. 2x2 행렬이기 때문에, 행렬식을 굉장히 쉽게 계산할 수 있겠죠. 때문에 r=-3 or 8이라는 고유값을 계산할 수 있습니다.

 이렇게 고유값을 계산하고 나면, 각각의 고유값에 대한 고유벡터를 계산할 수 있게 되겠죠. 여러분이 먼저 보셨던 예제처럼 말입니다.

 최초에 설명드렸던 것 처럼, A 라는 행렬과 r 라는 고유값은, 같은 방향을 가지되 크기가 다른 transformation을 시행하였습니다. 때문에 어떤 고유값 r에 대한 고유벡터 x에 대해, Ax를 시행한다는 것은, rx를 시행하는 것과 같고, 이는 시각적으로 아래와 같이, 방향은 유지하되 크기만 조절해주는, 그런 결과를 낳게됩니다.

 결국, 저희는 특성 방정식을 계산함으로써, 고유값을 계산하고, 해당 고유값에 맞는 고유벡터를 얻게되며, 이는 고유공간의 기저 벡터와 같게 됩니다. 이상입니다.

학습목표

 드디어 이번 강의에서는 이제까지 우리가 배워온 개념을 토대로 고유값 분해에 대해 배워보겠습니다. 그리고 고유값 분해를 통한 선형변환의 과정을 다루겠습니다.

핵심 키워드

• 고유값 분해(Eigen Decomposition)

학습하기

 그럼 이제, A matrix가 Diagonalizable이라고 가정해봅시다. 그럼 D=V^-1 A V로 표현할 수 있을테구요. 이는 다시 VDV^-1 = A라고 표현할 수 있을 테고, 이를 저희는 Eigen Decomposition이라고 부릅니다. 역행렬을 갖는 V 행렬과, Diagonal matrix D로 분해한거죠. 저희가 인수분해를 하듯, 어떤 행렬을 다른 행렬의 곱으로 표현하는 거죠. QR Factorization(Decomposition)처럼요. 

 다음과 같은 행렬 A가 있고, 이게 Linear transformation이라고 가정해봅시다. 그럼 Ax 를 계산하기 위해 V, D를 사용할 수 있습니다. 생각해봅시다. V는 고유벡터였죠. 그리고 Linear하기 때문에, af(x)+bf(y) = f(ax+by)라는 성질이 성립합니다. 그래서, 어떤 x가 들어왔을 때, 이것을 고유벡터의 선형결합으로 표현하게 되면, Ax라는 계산식을, rx라는 식으로 바꿔서 설명할 수 있게되고, 이것의 계산은 Ax에 비해 훨씬 간편하죠. 일종의 트릭인거죠.

 이러한 내용들을 더 잘 이해하기 위해, Change of Basis를 한 번 진행해봅시다. 전에 말씀드렸듯이, 기저는 하나로 고정되지 않습니다. 여러 가지의 기저가 존재할 수 있어요. 그 중에서도 Standard vector는 값을 표현하기에 굉장히 편리하죠. 그런데 저희가 하고싶은건, 어떤 벡터 x를 고유벡터의 선형결합으로 표현하는 겁니다. 그러니까 기저를 고유벡터로 변경하고자 하는거죠. v1 = [3,1], v2 = [-2,1]를 고유벡터로 갖는다고 가정하면, x = [4,3] = 2v1 + 1v2임을 알 수 있습니다. 여기서 2와 1이라는 Coefficient를 어떻게 찾는가-가 저희가 직면한 문제인겁니다. 사실 [4,3] = [v1, v2][x1, x2]를 풀면 되는 문제죠. 만약 [v1, v2]가 역행렬을 갖는다면, 이것의 역행렬을 양변에 곱해줌으로써 [x1, x2]를 도출할 수 있습니다. 이런 식으로 생각하셔도 좋습니다. Ax = V(D(V^-1x))를 떠올린 다음, 먼저, V^-1x를 생각해봅시다. y = V^-1x -> Vy = x. V = [v1, v2]이다. 쨋든, V의 역행렬이 존재하면 문제가 쉬워집니다. 물론 정방행렬이 아닌 등, 역행렬이 없으면 어떻게 하는가-하는 생각을 할 수 있지만, 애초에 저희는 V의 역행렬이 존재하는 가정이, Eigen Decomposition을 진행할 때 부터 깔려있습니다. 해서 V^-1x의 의미는, 그 자체로 고유벡터들의 선형결합으로 x를 표현하기 위한 계수를 계산하는 과정이 되는 겁니다.

 이제 D(V^-1x)를 다뤄보죠. D는 Diagonal matrix였습니다. 때문에 아래 그림에서 보실 수 있듯이, D와 y를 행렬곱한다는 것의 의미는, 단순히 y의 각 성분을 스칼라곱해주는 의미가 되는거죠. V^-1x = y가 x를 고유벡터의 선형결합으로 표현하기 위한 계수였는데, 이를 스칼라(고유값)곱해줌으로써, 그 길이만 변동시킨 셈입니다. 정확히는 해당 고유벡터에 대한 해당 고유값을 곱해준다는 의미겠죠.

 좌측이 y, 우측이 Dy에 대한 그림이 되겠죠.

 이제 마지막으로 VDy = Vz를 생각해봅시다. V는 고유벡터로 구성된 행렬입니다. 그리고 Dy = z는 고유벡터의 계수를 의미했습니다. 마지막으로 곱해지는 V의 역활은 고유벡터를 기저로 삼았던 좌표계를, 본래의 Standard basis 좌표계의 값으로 돌려놓는 역활을 하게 됩니다.

  결국 아래와 같은 계산이 성립하겠습니다.

 그래서, 결론적으로 다음과 같이 생각할 수 있습니다. Ax를 바로 계산 하는 것은, Eigen Decomposition을 통해 둘러둘러 계산할 수 있는데, V^-1를 통해 계수를 계산하고, D를 통해 고유값으로 간단히 계산하고, V를 통해 원래의 좌표계에 값을 표현한다. 가 되겠습니다.

 이제 A^k을 생각해봅시다. 예를 들어 A^10을 연산하고자하면, 곧이곧대로 하면, A를 10번이나 연산해야합니다. 그런데 이걸 Eigen Decomposition을 통해 연산해보면, 아래 수식과 같이 VD^kV^-1로 간단하게 표현할 수 있게 되죠. 좌표계를 여기갔다 저기갔다를 무수히 할 필요 없이, 한 번 고유벡터 좌표로 가서 모든 연산을 다 처리하고, 마지막으로 본래 좌표계로 돌아오는 겁니다. 그리고 D^k는 Diagonal matrix이기 때문에, 그 연산이 굉장히 단순해집니다.

Overview

                            *노란색 box로 쳐진 그림들이 생성된 결과 이미지*

Generative Adversarial Nets라는 제목으로 Ian Goodfellow 저자가 2014년 NIPS에서 게재된 논문이고 현재 약 42000건의 인용을 자랑할 만큼 그 당시에 획기적이였고, 생성모델의 줄기같은 논문. 현재도 많은 후속 연구들이 이어지고 있습니다.

참고 github 자료

Introduction

Deep generative model들은 maximum likelihood estimation과 관련된 전략들에서 발생하는 많은 확률 연산들을 근사하는 데 발생하는 어려움과 generative context에서는 앞서 모델 사용의 큰 성공을 이끌었던 선형 활성화 함수들의 이점들을 가져오는 것의 어려움이 있었기 때문에 큰 영향을 주진 못함. 이 논문에서 소개될 새로운 generative model은 이러한 어려움을 극복해냄.

• Generative model $G$ : Discriminative model이 구별할 수 없도록 training data의 분포를 모사
• Discriminative model $D$ : sample 데이터가 $G$로부터 나온 데이터가 아닌 실제 training data로부터 나온 데이터일 확률을 추정

본 논문에서는 생성 모델을 추정하는 새로운 프레임 워크를 제안합니다.
adversarial nets 프레임워크의 컨셉은 ‘경쟁’으로 Generative model G는 우리가 갖고 있는 data x의 distribution을 알아내려고 노력합니다. 만약 G가 정확히 data distribution을 모사할 수 있다면 거기서 뽑은 sample은 완벽히 data와 구별할 수 없게됩니다.
한편 discriminator model D는 현재 자기가 보고 있는 sample이 training data에서 온 것(진짜)인지 혹은 G로부터 만들어진 것인 지를 구별하여 각각의 경우에 대한 확률을 estimate합니다.

D의 입장에서는 data로부터 뽑은 sample $x$는 $D(x) = 1$이 되고, $G$에 임의의 noise distribution으로부터 뽑은 input $z$를 통해 생성된 sample에 대해서는 $D(G(z))=0$ 이 되도록 합니다. 즉 $D$는 실수할 확률을 낮추기위해 노력하고 반대로 $G$는 $D$가 실수할 확률을 높이기 위해 노력하는데, 본 논문에서는 이를 “_minimax two-player game_”이라고 표현합니다.

GAN의 경쟁하는 과정을 경찰(분류 모델, 판별자)과 위조지폐범(생성 모델, 생성자) 사이의 경쟁으로 비유하면 위조지폐범은 최대한 진짜 같은 화폐를 만들어 경찰을 속이기 위해 노력하고, 경찰은 진짜 화폐와 가짜 화폐를 완벽히 판별하여 위조지폐범을 검거하는 것을 목표로 합니다.
이러한 경쟁하는 과정의 반복은 어느 순간 위조 지폐범이 진짜와 다를 바 없는 위조지폐를 만들 수 있고 경찰이 위조 지폐를 구별할 수 있는 확률 역시 50%로 수렴하게 됨으로써 경찰이 위조 지폐와 실제 화폐를 구분할 수 없는 상태에 이르도록 합니다.

→ GAN의 핵심 컨셉은 각각의 역할을 가진 두 모델을 통해 적대적 학습(=경쟁)을 하면서 ‘진짜같은 가짜’를 생성해내는 능력을 키워주는 것!!

Adversarial nets

논문에서는 G와 D모델을 MLP를 활용해 구성하였습니다.

Generator’s distribution $p_g$ over data $x$를 학습하기 위해 generator의 input으로 들어갈 noise variables $p_z(z)$에 대한 prior를 정의하고 data space의 맵핑을 $G(z;θg)$라 표현할 수 있습니다.

여기서 $G$는 미분 가능한 함수로써 $θg$를 파라미터로 갖는 MLP입니다.

한편, Discriminator 역시 MLP으로 $D(x;θd)$ 로 나타내며 output은 확률이기 때문에 single scalar 값으로 나타남. $D(x)$는 $x$가 $p_g$가 아닌 data distribution으로부터 왔을 확률을 나타냅니다.

이를 수식으로 정리하면 다음과 같습니다.

• E_x~p_data(x)[logD(x)] : training data x를 D에 넣었을 때 나오는 결과를 log 취했을 때 얻는 기댓값을 의미
• E_z~p_z(z)[log(1-D(G(z)))] : noise distribution z를 G에 넣었을 때 나오는 결과를 D에 넣고 그 결과를 log(1-output) 했을 때 얻는 기댓값을 의미
• P_x~P_data(x) : G와 D에 들어가는 input이 무엇을 바탕으로 나왔는지 알려주는 표기. 즉 x가 p_data(x) → x는 training data에서 나온 분포라는 것을 의미

이 방정식을 D의 입장, G의 입장에서 각각 이해해본다면

→ 따라서 D의 입장에서 value function $V(D,G)$의 이상적인 최대값은 $0$ 이고 G의 입장에서 $V(D,G)$의 이상적인 최소값은 $-∞$ 임.

GAN은 discriminative distribution을 동시에 업데이트 하면서 학습하게 됩니다. 따라서 D는 sample distribution에서 비롯된 sample을 generative distribution으로 나온 sample로부터 판별하도록 학습합니다. 그림에서 $x, z$는 각각의 domain을 의미합니다.

이 그림이 말하고자 하는 것은 (a)처럼 real과 fake의 분포가 전혀 다르게 생긴 것을 볼 수있고, 현재 generator를 대상으로 discriminator를 학습시킨 결과가 (b)입니다.
(a)처럼 들쑥날쑥하게 확률을 판단하는 것이 아니라, 흔들리지 않고 나름 분명하게 확률을 결과로 내놓는 것을 알 수 있습니다. (a)보다 성능이 올라갔다고 표현할 수 있습니다.
어느정도 D가 학습이 이루어지면, G는 D가 구별하기 어려운 방향으로 학습을 하게되어 (c)와 같이 변하게 됩니다. 이 과정을 반복하게 되면 real과 fake가 점점 비슷해지고 결국에는 (d)와 같이 구분할 수 없게 되어 D가 확률을 0.5로 계산하게 됩니다.

→ 이 과정을 통해 진짜 이미지와 가짜 이미지를 구별할 수 없을 만한 데이터를 G가 생성해내는 것

Theoretical Results

아래를 k번 반복 (논문에서 k = 1로 실험)

1. m개의 노이즈 샘플을 pg(z)로부터 샘플링
2. m개의 실제 데이터샘플을 pdata(x)로부터 샘플링
3. V(G,D)식 전체를 최대화하도록 discriminator 파라미터 업데이트

이후

1. m개의 노이즈 샘플을 pg(z)로부터 샘플링
2. V(G, D)에서 log(1-D(G(z)))를 최소화 하도록 generator 파라미터 업데이트

Global Optimality of pg=pdata

어떤 G에서 optimal한 D가 존재한다고 생각한다면, G가 고정된 상태에서 optimal한 D는 다음과 같습니다

증명

D와 G를 학습시키는 criterion은 다음을 최대화 하는 것인데,

위의 식을 D(x)에 대해 편미분하고 결과값을 0이라고 두면 optimal한 D는 아래와 같이 얻어집니다

이렇게 얻은 optimal D를 원래의 목적함수 식에 대입하여 생성기 G에 대한 Virtual Training Criterion C(G)를 다음과 같이 유도할 수 있습니다.

위의 C(G)는 generator가 최소화하고자 하는 기준이 되며, 이것의 global minimum은 오직 $p_g = p_{data}$ 일때 달성되고 그 점에서의 C(G)값은 log4가 됩니다.

Cross entropy 교차엔트로피

정보 엔트로피는 하나의 확률분포가 갖는 불확실성(놀람의 정도) 혹은 정보량을 정량적으로 계산할 수 있도록 하는 개념을 나타내고 교차 엔트로피는 두 가지 확률 분포가 얼마나 비슷한지를 수리적으로 나타내는 개념입니다.

Convergence of Algorithm 1

G와 D가 충분한 capacity를 가지며, algorithm 1의 각 스텝에서 discriminator가 주어진 G에 대해 최적점에 도달하는게 가능함과 동시에 $$p_g$$가 위에서 제시한 criterion을 향상시키도록 업데이트 되는 한, $$p_g$$는 $$p_data$$에 수렴합니다.

• Convex : 아래로 볼록
• Concave : 위로 볼록
• sup : supremum , 상한

발표 자료

GAN 구현 코드

• tf.keras → Google Colaboratory
• torch → Google Colaboratory

증명 (추가)

G는 objective function을 최소화, D는 최대화시키며 각 네트워크를 학습시킨다는 것은 알겠는데, 서로 적대적으로 최대/최소화를 하며 optimal point에 도달할 수 있을까?

→ 답은 이미 나와 있다. 실제로 generator sample의 distribution과 real data distribution 사이의 간격을 최소화시켜서 0에 가깝게 만들기 때문에!!

즉, pg = pdata에 대한 global optimum을 가진다. → 이걸 objective function을 통해 증명해보자.

• Global optimum이 두 distribution(pg, pdata)가 같을 때임을 증명하기 위한 첫 번째 명제는, 최적화된, 즉 학습이 완료된 discriminator의 값이 위 명제와 같다는 것이다. (minmax에서 안쪽 maxD 먼저 계산해야함)
• 확률분포의 기댓값→적분 공식에 따라서 식은 적분 형태로 첫 번째 line과 같이 쓰일 수 있고, 두 번째 항 dz를 z→x space로 매핑하면 두 번째 line과 같이 g(z)→x, pz(z)→pg(x), dz→dx로 변환된다.
• 두 번째 line은 파란 박스 안의 식과 같은 형태를 가지는데, 저런 꼴의 식은 a/a+b에서 최대값을 가진다. (E.g. 참고)
• 따라서!!!!!! a=pdata, b=pg를 적용해보면, V를 최대화시키는 D는 위 명제와 같다는 것을 알 수 있고, 명제가 증명되었다.

D의 max값을 찾아서 이제 변수가 아니기 때문에 max=C(G)로 두고(새로운 함수. D 빠짐) 식을 다시 정리하면 위와 같다. 단순하게 구한 D를 대입한 결과이다.

• 여기까지 minmax 안쪽의 max를 계산했다. 이제 min을 계산해보자! 즉, min(C(G))를 찾아보자!

두 번째 명제는 pg=pdata인 경우에 C(G)가 global minimum을 가진다는 것이다. 즉, 우리가 원하는, 직관적으로 생각하는 이상적인 결과(pg=pdata)가 수식적으로도 global optimum이라는 것을 증명하는 것이다.

• 일단, 그냥 바로 pg=pdata를 앞에서 구한 D 식에 대입하면 D=1/2가 되겠고, 이어서 C(G)는 -log4의 값을 가진다. 이 -log4가 진짜 최솟값이라는 것을 확인하기 위한 마지막 증명이 다음 슬라이드이다. 끝까지 의심의 끈을 놓지 않는..!!

• line1: 구한 C(G)식을 다시 적고 기댓값을 적분으로 풀어주고, -log4를 빼고 더해준다.
• line2: log4를 log2+log2로 나눠서 분배해준다.
• line3: KL divergence의 식과 JSD의 식에 따라서, 마지막 line과 같이 정리된다.

KL, JSD: 간단히 말해서 두 분포 사이의 거리를 의미한다. 거리이기 때문에 최소값은 0이고, 양수이다.

• 따라서!!! 최종 식 -log4+JSD의 최소값은 -log4+0이고, JSD가 0이기 위해서는 두 분포 사이의 거리가 0인, pdata=pg일 때이다.

⇒ 최종 식 -log4+JSD를 통해서, minmax problem을 차례대로 풀어 global optimum을 찾으면, generator가 만드는 pg이 pdata와 정확히 일치하도록 할 수 있다는 것을 알 수 있다!

⇒ 결국 generator로부터 뽑은 sample을 discriminator가 실제 데이터와 구별할 수 없게 되었다는 것이다. = 우리가 원하는 결과임

Product Serving

강의의 목표

• AI 엔지니어가 되기 위한 기본 소양을 갖추기
• 문제 정의에 대해 고민을 하는 사람

1. MLOps 개론

모델 개발 프로세스 - Research

• 문제정의 - EDA - Feature Engineering - Train - Predict

모델 개발 프로세스 - Production

• 문제정의 - EDA - Feature Engineering - Train - Predict - Deploy

✨MLOps의 목표는 빠른 시간 내에 가장 적은 위험을 부담하며 아이디어 단계부터 Production 단계까지 ML 프로젝트를 진행할 수 있도록 기술적 마찰을 줄이는 것✨

1. MLOps가 필요한 이유 이해하기

   • Production을 하기 위한 과정임으로 중요함

2. MLOps의 각 Componenet에 대해 이해하기

   • Server infra = 어떻게 server를 이용할 지에 대한 고민
   • GPU infra = 가동하려는 모델과 회사 운영자원 및 개발환경에 맞게끔 설정
   • Serving = 실질적으로 소비자에게 어떤 방식으로 전해질지
   • Experiment, Model Management = Model test 및 성능 개선을 위한 파라미터 튜닝, 다양한 모델 테스트
   • Feature Store = 필요한 모델 템플릿 만들기
   • Data Validation = 데이터 검증(기존 데이터, Train 데이터와의 차이 확인)
   • Continuous Training = 지속적인 성능 개선
   • Monitoring = 모아지는 데이터를 분석하고 여기서 결과를 얻어 이를 활용해 개선방향 도모
   • AutoML = 자동으로 성능 튜닝

3. MLOps 관련된 자료, 논문 읽어보며 강의 내용 외에 어떤 부분이 있는지 파악해보기

   • https://github.com/EthicalML/awesome-production-machine-learning

4. MLOps Component 중 내가 매력적으로 생각하는 TOP3을 정해보고 왜 그렇게 생각했는지 작성해보기

   • Server infra 와 GPU infra가 가장 중요하다고 여기고 그 이유는 아무래도 직접적인 회사 운영에 가장 큰 영향이 드는 금전적인 부분을 담당하고 있기 때문에 이 두개의 Component에서 비용을 절감한다면 그 잔여비용으로 다른 Component 개선에 큰 영향을 줄 수 있을 것이라고 생각함. 또 마지막으로 Monitoring을 통해 앞으로 나아갈 방향성과 개선점에 대해서 얻을 수 있어서 중요하다고 생각함.

모델 경량화

1.1 경량화를 왜 해야 하나요?

On device AI

• 제한된 리소스내에서 AI를 활용하기 위해서는 경량화가 필수!

AI on cloud(or server)

• 배터리, 저장 공간, 연산능력의 제약은 줄어드나, latency와 throughtput의 제약이 존재
• 같은 자원(=돈)으로 더 적은 latency와 더 큰 throughput이 가능하다면?

Computation as a key component of AI progress

경량화는 ?

• 모델의 연구와는 별개로, 산업에 적용되기 위해서 거쳐야하는 과정
• 요구조건(하드웨어 종류, latency 제한, 요구 throughput, 성능)들 간의 trade-off를 고려하여 모델 경량화/최적화를 수행

1.2 경량화 분야 소개

1. Efficient architecture

• 매년 쏟아져 나오는 블록 모듈들
• 각 모듈 블록마다의 특성이 다름! (성능, 파라미터 수, 연산횟수 등..)

Efficient architecture design; AutoML, Neural Architecture Search

• Software 1.0 : 사람이 짜는 모듈
• Software 2.0 : 알고리즘이 찾는 모듈

2. Network Pruning; 찾은 모델 줄이기

• 중요도가 낮은 파라미터를 제거하는 것
• 좋은 중요도를 정의, 찾는 것이 주요 연구 토픽 중 하나 (e.g. L2 norm이 크면, loss gradient 크면, 등등..)
• 크게 structured/unstructured pruning으로 나뉘어짐

Network Pruning; Structured pruning

• 파라미터를 그룹 단위로 pruning하는 기법들을 총칭(그룹; channel / filter,layer 등)
• Dense computation에 최적화된 소프트웨어 또는 하드웨어에 적합한 기법

• channel scaling factor = 중요도

Network Pruning; Structured pruning

• 파라미터 각각을 독립적으로 pruning하는 기법
• Pruning을 수행할 수록 네트워크 내부의 행렬이 점차 희소(sparse)해짐
• Structured Pruning과 달리 sparse computation에 최적화된 소프트웨어 또는 하드웨어에 적합한 기법

3. Knowledge distillation

• 학습된 큰 네트워크를 작은 네트워크의 학습 보조로 사용하는 방법
• Soft target(soft outputs)에는 ground truth 보다 더 많은 정보를 담고 있음
  (e.g 특정 상황에서 레이블 간의 유사도 등등)

• 1) Student network와 ground truth label의 cross-entropy
• 2) teacher network와 student network의 inference 결과에 대한 KLD loss로 구성

• T는 Large teacher network의 출력을 smoothing(soften)하는 역할을 한다.
• a는 두 loss의 균형을 조절하는 파라미터다.

4. Matrix/Tensor decomposition

• 하나의 Tensor를 작은 Tensor들의 operation들의 조합(합, 곱)으로 표현하는 것
• Cp decomposition : rank 1 vector들의 outer product의 합으로 tensor를 approximation

Network Quantization

• 일반적인 float32 데이터타입의 Network의 연산과정을 그보다 작은 크기의 데이터타입
  (e.g float16, int8, ...)으로 변환하여 연산을 수행

• 사이즈 : 감소
• 성능(Acc) : 일반적으로 약간 하락
• 속도 : Hardware 지원 여부 및 사용 라이브러리에 따라 다름(향상 추세)
• Int8 quantization 예시(CPU inference, 속도는 pixel2 스마트폰에서 측정됨)

6. Network Compiling

• 학습이 완료된 Network를 deploy하려는 target hardware에서 inference가 가능하도록 compile하는 것(+ 최적화가 동반)
• 사실상 속도에 가장 큰 영향을 미치는 기법
• e.g TensorRT(NVIDIA), Tflite(Tensorflow), TVM(apache), ...
• 각 compile library마다 성능차이가 발생

• Compile 과정에서, layer fusion(graph optimization) 등의 최적화가 수행됨
• 예를들어 tf의 경우 200개의 rule이 정의되어 있음

• Framework와 hardware backends 사이의 수많은 조합
• HW마다 지원되는 core, unit 수, instruction set, 가속 라이브러리 등이 다름
• Layer fusion의 조합에 따라 성능차이가 발생 (동일 회사의 hw 임에도 불구하고!)

• AutoML로 graph의 좋은 fusion을 찾아내자!
• e.g. AutoTVM(Apache)

데이터 제작의 중요성 2

1. Life Cycle of an AI Project

AI Research vs AI Production

보통 수업/학교/연구에서는 정해진 데이터셋/평가 방식에서 더 좋은 모델을 찾는 일을 함.

하지만 서비스 개발 시에는 데이터 셋은 준비되어 있지 않고 요구사항만 존재함!

그래서 서비스에 적용되는 AI 개발 업무의 상당 부분이 데이터셋을 준비하는 작업임🙄!

Production Process of AI Model

서비스향 AI 모델 개발 과정은 크게 4가지로 구성되어 있음!

이 과정의 목표는 요구사항을 충족시키는 모델을 지속적으로 확보하는 것이고 방법으로는 두가지가 있음!

모델 성능 달성에 있어서 데이터와 모델에 대한 비중은 어떨까!?

그렇다면 사용 중인 모델의 성능 개선 시에는 데이터와 모델에 대한 비중은 어떻게 바뀔까!?

1. 서비스 출시 후에는 정확도에 대한 성능 개선 요구가 제일 많음
2. 이 때 정확도 개선을 위해 모델 구조를 변경하는 것은 처리속도, qps, 메모리 크기 등에 대한 요구사항에 검증도 다시 해야 하므로 비용이 큼

2. Data! Data! Data!

2.1 Data-related tasks

예상보다 데이터와 관련된 업무가 왜 이렇게 많을까!?

1. 어떻게 하면 좋을지에 대해서 알려지 있지 않다!

   • 학계에 나오는 논문의 대부분은 모델(구조/학습방법)에 관련된 논문
   • 학계에서 데이터를 다루기 힘든 이유 -> 좋은 데이터 모으기 힘듬, 라벨링 비용이 큼, 작업 기간이 김.

2. 데이터 라벨링 작업은 생각보다 많이 많이 어렵다!

   • 데이터가 많다고 모델 성능이 항상 올라가는 것은 아님😮
   • 라벨링 결과에 대한 노이즈 = 라벨링 작업에 대해 일관되지 않음의 정도
   • 잘못 작업된 라벨링 결과를 학습 시 무시하게 하려면 적어도 깨끗이 라벨링된 결과가 2배 이상 필요
     • 라벨링 노이즈를 상쇄할 정도로 깨끗한 라벨링 데이터가 골고루 일정하게 많아야 한다!

3. 데이터 불균형을 바로 잡기가 많이 어렵다!

이 작업을 효율화 하기 위한 방법

• 해당 task에 대 한 경험치가 잘 쌓여야 하므로 결국 도메인 지식이 많을 수록 예외 경우에 대해서 미리 인지를 할 수 있어야함!

데이터 제작의 중요성

데이터 제작의 중요성

Software 1.0

Software 1.0은 다음의 개발 과정을 따름

1. 문제 정의
2. 큰 문제를 작은 문제들의 집합으로 분해
3. 개별 문제 별로 알고리즘 설계
4. 솔루션들을 합쳐 하나의 시스템으로

하지만 객체 검출에서 대응하기 어려운 케이스가 정말 많았음..😥

이에 대한 해결책으로 결국 Software 2.0이 등장!!

사람의 개입이 없이 어떻게 특정 연산들이 정의될까..?

Software 2.0은 뉴럴넷의 구조에 의해 검색 영역이 정해지고 최적화를 통해 사람이 정한 목적에 제일 부합하는 연산의 집합을 찾음.

이때 경로와 목적지는 데이터와 최적화 방법에 의해 정해짐.

요약

• Software 1.0은 사람이 고민하여 프로그램을 만든 것!
• Software 2.0은 AI 모델의 구조로 프로그램의 검색 범위를 한정하고, 데이터와 최적화 방법을 통해 최적의 프로그램을 찾는 것!