부스트캠프 AI Tech 2기 - 3 (1)

통계학

데이터를 보고 확률분포 가정하기.

• 확률 분포를 가정하는 방법 : 히스토그램을 통해 모양을 관찰
  • 데이터가 2개의 값 ( 0 또는 1 ) 만 가지는 경우 -> 베르누이분포

![image](https://user-images.githubusercontent.com/61610411/128133910-e91ed48e-67d2-4d40-aaf6-42da2e06b6f2.png)


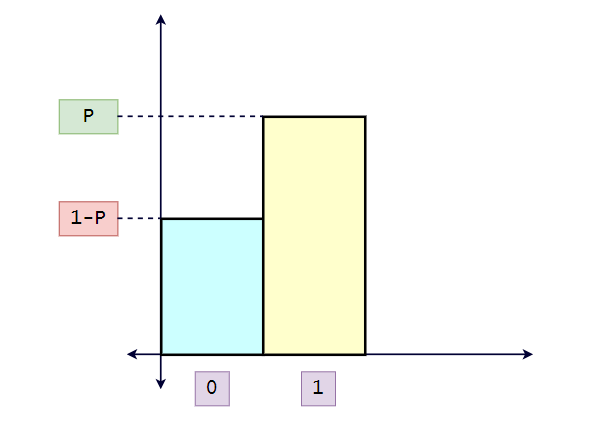
- 데이터가 n개의 이산적인 값을 가지는 경우 -> **카테고리분포**


![image](https://user-images.githubusercontent.com/61610411/128149550-4cf5ed86-0169-4a06-afd7-0ca739a3ae8d.png)


- 데이터가 (0,1) 사이에서 값을 가지는 경우 -> **베타분포**


![image](https://user-images.githubusercontent.com/61610411/128149845-fc7578f7-0a37-495a-b22f-a13c51767b0c.png)


- 데이터가 0 이상의 값을 가지는 경우 -> **감마분포, 로그정규분포 등**


![image](https://user-images.githubusercontent.com/61610411/128150065-e19e83fa-8528-49df-8b1e-9ed6b0fffbdb.png)


- 데이터가 실수 전체에서 값을 가지는 경우 -> **정규분포, 라플라스분포 등**


![image](https://user-images.githubusercontent.com/61610411/128150794-7208d2b8-8d33-4a52-ab16-474b5737492f.png)

• 기계적으로 확률분포를 가정해서는 안 되며, 데이터를 생성하는 원리를 먼저 고려하는것이 원칙

---

중심극한정리(Central Limit Thorem)

• 동일한 확률 분포를 가진 독립 확률 변수 n개의 평균의 분포는 n개가 커짐에 따라
  모집단 분포의 모양에 관계없이 정규분포와 가까워지는 정리

---