Generative Model

Auto-regressive model

NADE

Gaussian Mixture Model

Pixel RNN

Taxonomy of Machine Learning

GAN 모델을 설명하기 전에 딥러닝을 크게 두 가지로 나누면, Supervised Learning과 Unsupervised Learnging이 있다.

• Supervised Learning 지도 학습

대표적인 모델로 Discriminative Model이 있으며, 로지스틱 회귀분석, 뉴럴 네트워크 등이 해당된다. input에 해당하는 클래스를 맞추기 위해 학습하게 된다.

• Unsupervised Learning 비지도 학습

label이 없는 데이터를 잘 학습하는 것이다 Generative Model에는 Naive Bayes, Gaussian discriminanat analysis (GDA, 가우시안 판별분석)이 있다. 학습데이터에서 분포를 학습 한 뒤, 학습 데이터와 유사한 데이터를 만드는게 목표이다. 학습이 진행될 수록 실제 데이터와 생성한 데이터의 분포가 유사해진다.

파란색은 학습셋 데이터의 불포이며, 빨간색은 모델이 생성한 이미지의 분포이다. 데이터의 분포를 실제와 근사하게 만드는게 Generative Model의 목표이다.

Generative Adversarial Networks

Generative Adversarial Networks는 편의상 GAN, 겐, 간으로도 부른다. Adversarial Network는 적대적인 신경망이 서로 경쟁하면서 가짜 모델의 성능을 개선한다.

Discriminator는 진짜 이미지를 진짜(1)로, 가짜를 가짜(0)로 구분하도록 학습한다. 반대로, generator(Neural Network)는 랜덤한 코드를 통해서 이미지를 생성하며, Discriminator를 속여 가짜 이미지를 진짜처럼 만드는게 목표이다. 즉, 실제 데이터의 분포와 모델이 생성한 데이터의 분포 간의 차이를 줄이는 것이다.

GAN을 처음 제안한 lan Goodfellow는 <경찰과 위조지폐범>으로 비유하였다.

지폐위조범이 처음에는 돈을 제대로 못 만들어 경찰이 위조지폐를 제대로 구분하여 검거에 성공했다. 이 후, 지폐위조범은 더욱 발전된 기술로 지폐를 위조한다. 위조지폐범은 진짜 같은 위조지폐를 만들어(생성, generator) 경찰을 속이고, 경찰은 진짜와 가짜 화폐를 구분(분류, discriminator)하기 위해 노력한다.

결국 위조지폐범은 구분하기 어려운 위조지폐를 만들게 된다. 경찰은 이게 진짜인지 가짜인지 구별하기 가장 어려운 50% 확률로 수렴하게 된다.

모델 관점에서 다시 해석하면, generator에서 input에서 쓰레기(garbage) 값을 보내도 output(위조지폐, 실제는 이미지)은 실제와 가짜를 구분할 수 없게끔(adversarial) 만들게 된다.

1. Generator는 기존 샘플(training, real) 분포를 파악하여 새로운 샘플(fake)을 생성한다.

2. Discriminator는 샘플이 Generator 또는 Training 중 어디에서 온건지 확률을 평가함 (Minimax tow-player game)

3. Generator 가 Discriminator 분포를 완벽한 수준으로 복원하면 Discriminator가 generator의 산출물(fake)와 Training(real) 을 구분할 확률은 1/2가 된다.

Theoretical Results

• Q_model(x|z) : 정의하고자 하는 z값을 줬을때 x 이미지를 내보내는 모델

• P_data(x) : x 라는 data distribution은 있지만 어떻게 생긴지는 모르므로, P 모델을 Q 모델에 가깝게 가도록 한다.

• 파란점선 --- : discriminator distribution (분류 분포) > 학습을 반복하다보면 가장 구분하기 어려운 구별 확률인 1/2 상태가 된다.

• 녹색 선 - : generative distribution (가짜 데이터 분포)

• 검은색 점선 --- : data generating distribution (실제 데이터 분포)

Minimax Problem of GAN

Theoretical Results

위에 정의한 Minimax problem (최소최대문제)가 실제로 풀 수 있는 문제인지 확인이 필요하다. 이를 위해 (1) 실제 정답이 있는지 (existence)와 (2) 해가 존재한다면 유일한지 (uniqueness) 검증이 필요하다.

Two Step Approach

아래 두 가지를 증명해야 우리가 원하는 바를 해결할 수 있다고 볼 수 있다.

1. Global Optimality of P_g = P_data
   GAN의 Minimax problem이 global optimality를 가지고 있다.
   P_data (data distribution)이 generative한 model distribution이 정확히 일치할 때 global optimality 이며, 그때 global optimality(P_g = P_data)를 갖는가?

2. Convergence of Algorithm 1
   우리가 제안하는 알고리즘(discrimiator <-> distribution model 학습하는 과정의 모델)이 실제로 global optimality(P_g = P_data)을 찾을 수 있는가?

   

   실제 데이터 분포와 모델 분포 간의 거리가 최소이기 때문에 GAN은 성립한다.

Adventages and Disadventages

A. Adventages

1. 기존의 어떤 방법보다도 사실적인 결과물을 만들 수 있음

2. 데이터의 분포를 학습하기 때문에, 확률 모델을 명확하게 정의하지 않아도 Generator가 샘플(fake)을 생성할 수 있음

3. MCMC(Markov Chain Monte Carlo)를 사용하지 않고, backprop을 이용하여 gradient를 구할 수 있음(한번에 샘플을 생성 가능)

4. 네트워크가 매우 샤프하고 degenerator(변형된) 분포를 표현할 수 있음.
   Markov Chain 기반 모델에서는 체인 간에 혼합될 수 있도록 분포가 다소 선명하지 않음

5. Adversarial model은 generator의 파라미터가 샘플 데이터에 의해 직접 업데이트 하지 않고, disciminator의 gradient를 이용하여 통계적 이점을 얻음

MCMC(Markov Chain Monte Carlo) 는 어떤 목표 확률분포(Target Probability Distribution)로 부터 랜덤 샘플을 얻는 방법이다.

MCMC를 이해하기 위해서는 마코프 연쇄(Markov Chain)과 Monte Carlo 두 가지 개념을 이해해야 한다.

마코프 연쇄는 시간에 따른 계의 상태의 변화를 나타내며, 매 시간마다 계는 상태를 바꾸거나 같은 상태를 유지하며 상태의 변화를 '전이'라고 한다. 마르코프 성질은 과거와 현재 상태가 주어졌을 때의 미래 상태의 조건부 확률 분포가 과거 상태와는 독립적으로 현재 상태에 의해서만 결정된다는 것을 뜻한다.

몬테 카를로 방법은 난수를 이용하여 함수의 값을 확률적으로 계산하는 알고리즘을 부르는 용어이다. 수학이나 물리학 등에서 자주 사용된다. 이 방법은 계산하려는 값이 닫힌 형식(closed form)으로 표현되지 않거나 매우 복잡한 경우에 확률/근사적으로 계산할 때 사영되며 유명한 도박의 도시 몬테 카를로의 이름을 본따 만들어 졌다.

B. Difficulties & Disadvantage

1. Simple Example : unstable
   Minimax 최적화 문제를 해결하는 과정이기 때문에, oscillation이 발생하여 모델이 불안정 할 수 있다.
   -> 두 모델의 성능 차이가 있으면 한쪽으로 치우치기 때문에 DCGAN(Deep Convolution GAN)으로 문제 개선

2. Minibatch Discrimination
   컨버전스가 안되는 경우는 여러 케이스를 보여준다. (use other examples as side information)

3. Ask Somebody
   평가를 어떻게 해야할까? 정말 사람 같은 이미지라고 평가할 수 있지만 주관적이다. 또한, 언제 멈춰야 되는지에 대한 기준이 부족하다.
   -> Inception score 사용하여 문제 해결
   : classification 하는 모델에 학습이 끝난 모델에서 나온 샘플을 넣어서 클래스가 잘 나오는지 (=하나의 클래스로 분류하는지)에 따라서 점수를 측정한다.

4. Mode Collapes (sample diversity)
   :minmaxGD = maxminDG ->

   • Generator 입장에서는 Discriminator가 가장 성능이 안좋게 판단한 최소값 하나만 보내주면 됨
   • 예를 들어, 1~10 을 학습할 때 1의 성능이 좋지 않다면 1만 보내주다가, 나중에는 1은 무조건 실제가 아닌것으로 판단함.[Unrolled-Generative-Adversarial-Model]https://arxiv.org/abs/1611.02163

5. 학습 데이터의 분포를 따라가기 때문에 어떤 데이터가 생성될지 예측하기 어려움
   -> cGAN(Condtional GAN)을 이용하여 문제 개선

6. HELvetica scenario 를 피하기 위해 G는 D가 업데이트 하기 전에 학습을 너무 많이하면 안됨
   Helvetica scenario : generator가 서로 다른 z들을 하나의 output point로 맵핑할 때 발생하는 문제
   [kangbk0120.github.io/articles/2017-08/tips-from-goodfellow]<kangbk0120.github.io/articles/2017-08/tips-from-goodfellow>

GAN PyTorch Implementation

MNIST를 활용하여 GAN을 구현하는 방법은 [Woosung Choi's blog <GAN PyTorch 구현: 손글씨 생성>]https://ws-choi.github.io/blog-kor/seminar/tutorial/mnist/pytorch/gan/GAN-%ED%8A%9C%ED%86%A0%EB%A6%AC%EC%96%BC/ 에서 확인

참고자료 : (https://wegonnamakeit.tistory.com/54),(https://www.youtube.com/watch?v=odpjk7_tGY0&t=69s),(https://www.youtube.com/watch?v=L3hz57whyNw&feature=youtu.be)

Transformer

Sequential data 의 어려운점

• 입력 데이터가 길고 길이가 일정하지 않을 수 있다.
• 입력 심볼의 다양성. 입력신호를 어떤 단위화된 심볼로 본다면 그 다양성이 매우 크다. 심볼의 크기도 시간 단위, 혹은 윈도우 크기를 무엇으로 정하냐에 따라 많은 심볼이 가능하다.
• 긴시간 동산의 context 학습이 필요하다.
• 심볼 간의 dependency도 학습이 필요하다. 어떠한 심볼들의 순차적 출현이 중요한 패턴일지 습해야 하므로 꼭 학습이 필요하다.

Transformer

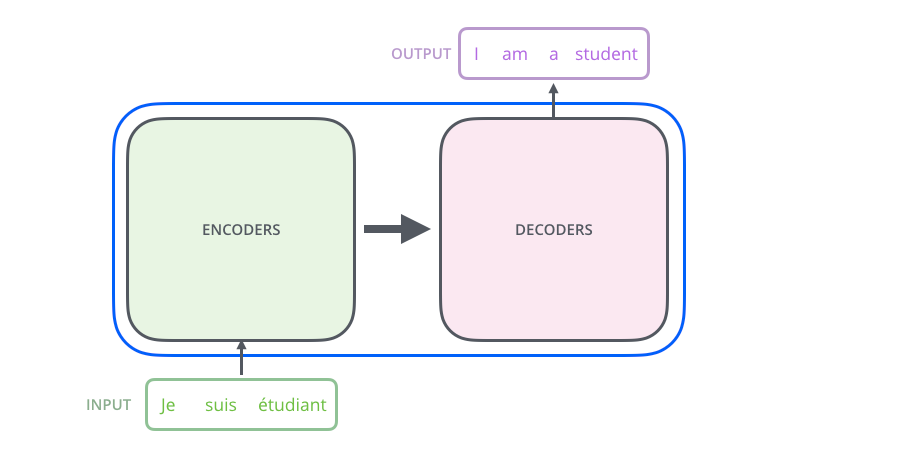
모델의 자세한 부분을 무시하고 이를 하나의 black box 라고 보자. 기계 번역의 경우를 생각해본다면, 모델은 어떤 한 언어로 된 하나의 문장을 입력으로 받아 다른 언어로 된 번역을 출력으로 내놓을 것이다.

그 black box를 열어 보게 되면 우리는 encoding 부분, decoding 부분, 그리고 그 사이를 이어주는 connection들을 보게 된다.

encoding 부분은 여러개의 encoder 를 쌓아 올려 만든 것이다. (논문에서는 6개를 쌓았다고 하나, 꼭 6개를 쌓아야 하는 것은 아니고 각자의 세팅에 맞게 얼마든지 변경하여 실험할 수 있다.) decoding 부분은 encoding 부분과 동일한 개수만큼의 decoder를 쌓은 것을 말한다.

encoder 들은 모두 정확히 똑같은 구조를 가지고 있다. 그러나 그들 간의 같은 weight를 공유하진 않는다. 하나의 encoder를 나눠보면 아래와 같이 두개의 sub-later로 구성되어 있다.

인코더에 들어온 입력은 일단 먼저 self-attention layer를 지나가게 된다. 이 layer는 encoder가 하나의 특정한 단어를 encode 하기 위해서 입력 내의 모든 다른 단어들과의 관계를 살펴본다.

입력이 self-attention 층을 통과하여 나온 출력은 다시 feed-forward 신경망으로 들어가게 된다. 똑같은 feed-forward 신경망이 각 위치의 단어마다 독립적으로 적용돼 출력을 만든다.

decoder 또한 encdoer에 있는 두 layer를 모두 가지고 있다. 그러나 그 두 층 사이의 seq2seq 모델의 attention과 비슷한 encoder-decoder attention이 포함되어 있다. 이는 decoder가 입력 문장 중에서 각 타임 스텝에서 가장 관려 있는 부분에 집중할 수 있도록 해준다.

벡터들을 기준으로 그림 그려보기

이제 우리는 Transformer 모델의 주요 부분들에 대해서 다 알아보았다. 이제 입력으로 들어와서 출력이 될때까지 이 부분들 사이를 지나가며 변환될 벡터/ 텐서들을 기준으로 모델을 살펴보자.

현대에 들어 대부분 NLP 관련 모델에서 그러듯, 먼저 입력 단어들을 embedding 알고리즘을 이용해 벡터로 바꾸는 것부터 해야 한다.

각 단어들은 크기 512의 벡터 하나로 embed된다. 우리는 이 변환된 벡터들을 위와 같은 간단한 박스로 나타낸다.

이 embedding은 가장 밑단의 encoder에서만 일어난다. 이렇게 되면 우리는 이렇게 뭉뚱그려 표현할 수 있게 된다. 모든 encoder들은 크기 512의 벡터의 리스트를 입력으로 받는다. 이 벡터는 가장 밑단의 encoder의 경우에는 word embedding이 될 것이고, 다른 encoder들에서는 바로 전의 encoder의 출력이 될 것이다. 이 벡터 리스트의 사이즈는 hyperparameter로 우리가 마음대로 정할 수 있다. 가장 간단하게 생각한다면 우리의 학습 데이터 셋에서 가장 긴 문장의 길이로 둘 수 있다.

입력 문장의 단어들을 embedding 한 후에, 각 단어에 해당하는 벡터들을 encoder 내의 두 개의 sub-layer으로 들어가게 된다.

여기서 우리는 각 위치에 있는 그 단어가 그만의 path를 통해 encoder에서 흘러간다는 Transformer 모델의 주요 성질을 볼 수있다. Self-attention 층에서 이 위치에 따른 path들 사이에 다 dependency가 있다. 반명 feed-forward 층은 이런 dependency가 없기 때문에 feed-forward layer 내의 이 다양한 path 들은 병렬처리될 수 있다.

Encoding

앞서 설명한것과 같이, encoder는 입력으로 벡터들의 리스트를 받는다. 이 리스트를 먼저 self-atttention layer에, 그 다음으로 feed-forward 신경망에 통과 시키고 그 결과물을 그 다음 encoder에게 전달한다.

각 위치의 단어들은 각각 다른 self-encoding 과정을 거친다. 그 다음으로는 모두에게 같은 과정인 feed-forward 신경망을 거친다.

Self-Attention 자세히 보기

이번 섹션에서는 먼저 여러가지 벡터들을 통해서 어떻게 self-attention을 계산할 수 있는지 볼 것이다. 그 후 행렬을 이용하여 이것이 실제로 어떻게 구현돼 있는지 확인해보자.

self-attention 계산의 가장 첫 단계는 encoder에 입력된 벡터들(이 경우에서는 각 단어의 embedding 벡터이다)에게서 부터 각 3개의 벡터를 만들어 내는 일이다. 우리는 각 단어에 대해서 Query 벡터, Key 벡터, 그리고 Value 벡터를 생성한다. 이 벡터들은 입력 벡터에 대해서 세개의 학습 가능한 행렬들을 각각 곱함으로써 만들어진다.

여기서 한가지 짚고 넘어갈 것은 이 새로운 벡터들이 기존의 벡터들 보다 더 작은 사이즈를 가진다는 것이다. 기존의 입력 벡터들은 크기가 512인 반면 이 새로운 벡터들은 크기가 64이다. 그러나 그들이 꼭 이렇게 더 작아야만 하는 것은 아니며, 이것은 그저 multi-head attention의 계산 복잡도를 일정하게 만들고자 내린 구조적인 선택일 뿐이다.

x1를 weight 행렬인 WQ로 곱하는 것은 현재 단어와 연관된 query 벡터린 q1을 생성한다. 같은 방법으로 우리는 입력 문장에 있는 각 단어에 대한 query, key, value 벡터를 만들 수 있다.

그렇다면 정확히 이 query, key, value 벡터란 무엇을 의미하는 것일까?

그것은 attention 에 대해서 생각하고 계산하려할 때 도움이 되는 추상적인 개념이다. 이제 곧 다루게 될 테지만 어떻게 attention 이 실제로 계산되는지를 알게 되면, 자연스럽게 세 개 의 벡터들이 어떤 역할을 하는지 알 수 있게 된다.

self-attention 계산의 두 번째 스텝은 점수를 계산하는 것이다. 아래 예시의 첫번째 단어인 "Thinking"에 대해서 self-attention 을 계산한다고 하자. 우리는 이 단어와 입력 문장 속의 다른 모든 단어들에 대해서 각각 점수를 계산해야 한다. 이 점수는 현재 위치의 이 단어를 encode 할 때 다른 단어들에 대해서 얼마나 집중을 해야 할지를 결정한다.

점수는 현재 단어의 query vector와 점수를 매기려 하는 다른 위치에 있는 단어의 key vector의 내적으로 계산된다. 다시말해, 우리가 위치 #1에 있는 단어에 대해서 self-attention 을 계산한다 했을 때, 첫 번째 점수는 q1과 k1의 내적일 것이다. 그리고 동일하게 두번째 점수는 q1과 k2 의 내적일 것이다.

세번째와 네번째 단계는 이 점수들을 8로 나누는 것이다. 이 8이란 숫자는 key 벡터의 사이즈인 64의 제곱근이라는 식으로 계산이 된 것이다. 이 나눗셈을 통해 우리는 더 안정적인 gradient를 가지게 된다. 그리고 난 다음 이 값을 softmax 계산을 통과시켜 모든 점수를 양수로 만들고 그 합을 1로 만들어 준다.

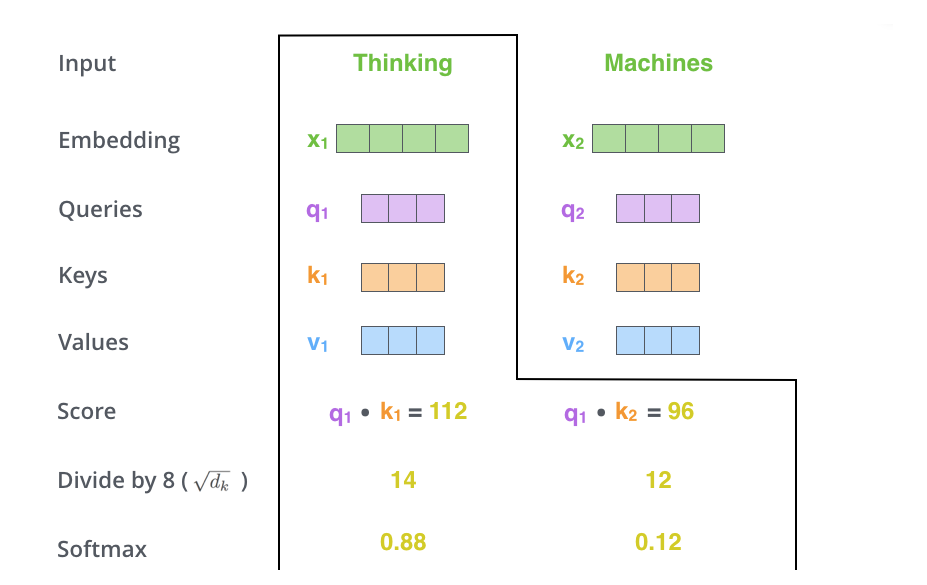
이 softmax 점수는 현재 위치의 단어의 encoding에 있어서 얼마나 각 단어들의 표현이 들어갈 것 인지를 결정한다. 당연하게 현재 위치의 단어가 가장 높은 점수를 가지며 가장 많은 부분을 차지하게 되겠지만, 가끔은 현재 단어에 관련이 있는 다른 단어에 대한 정보가 들어가는 것이 도움이 된다.

다섯 번째 단계는 이제 입력의 각 단어들의 value 벡터에 이 점수를 곱하는 것이다. 이것을 하는 이유는 우리가 집중을 하고 싶은 관련이 있는 단어들을 그래도 남겨두고, 관련이 없는 단어들은 0.001과 같은 작은 숫자(점수)를 곱해 없애버리기 위함이다.

마지막 여섯 번째 단계는 이 점수로 곱해진 weighted valuie 벡터들을 다 합해 버리는 것이다. 이 단계의 출력이 바로 현재 위치의 대한 self-attention layer의 출력이 된다.

이 여섯 가지 과정이 바로 self-attention의 계산 과정이다. 우리는 이 결과로 나온 벡터를 feed-forward 신경망으로 보내게 된다. 그러나 실제 구현에서는 빠른 속도를 위해 이 모든 과정들이 벡터가 아닌 행렬의 형태로 진행하게 된다. 우리는 이 때까지 각 단어 레벨에서의 계산과 그 이유에 대해서 얘기해봤다면, 이제 이 행렬 레벨의 계산을 살펴보도록 하자.

Self-attention 의 행렬 계산

가장 첫 스텝은 입력 문장에 대해서 Query, Key, Value 행렬들을 계산하는 것이다. 이를 위해 우리는 우리의 입력 벡터들 (혹은 embedding 벡터들)을 하나의 행렬 X로 쌓아 올리고, 그것을 우리가 학습할 weight 행렬들인 WQ, WK, WV로 곱한다.

행렬 X의 각 행은 입력 문장의 각 단어에 해당합니다. 우리는 여기서 다시 한번 embedding 벡터들(크기 512, 그림에서는 4)과 query,key,value 벡터들(크기 64, 그림에서는 3) 간의 크기 차이를 볼 수있다.

마지막으로 우리는 현재 행렬을 이용하고 있으므로 앞서 설명했던 self-attention 계산 단계 2부터 6까지를 하나의 식으로 압축 할 수 있다.

The Beast With Many Heads

본 논문은 이 self-attention layer 에다 "multi-headed" attention 이라는 메커니즘을 더해 더욱 더 이를 개선한다. 이것은 두 가지 방법으로 attention later의 성능을 향상시킨다.

1. 모델이 다른 위치에 집중하는 능력을 확장시킨다.
2. attention layer가 여러개의 "representation 공간"을 가지게 해준다.

multi-headed attention을 이용하기 위해서 우리는 각 head를 위해서 각각의 다른 query/key/value weight 행렬들을 모델에 가지게 된다. 이전에 설명한 것과 같이 우리는 입력 벡터들의 모음인 행렬X를 WQ/WX/WV 행렬들로 곱해 각 head에 대한 Q/K/V행렬들을 생성한다.

위에 설명했던 대로 같은 self-attention 계산 과정을 8개의 다른 weight 행렬들에 대해 8번 거치게 되면, 우리는 8개의 서로 다른 Z 행렬을 가지게 된다.

그러나 문제는 이 8개의 행렬을 바로 feed-forward layer으로 보낼 수 없다는 것이다. feed-forward layer 은 한 위치에 대해 오직 한 개의 행열만을 input으로 받을 수 있다. 그러므로 우리는 이 8개의 행렬을 하나의 행렬로 합치는 방법을 고안해 내야 한다.

어떻게 할 수 있을까? 간단하다. 일단 모두 이어 붙여서 하나의 행렬로 만들어버리고 그 다음 하나의 또 다른 weight 행렬인 W0을 곱해버린다.

사실상 multi-headed self-attention 은 이게 전부이다.
이제 이 모든 것을 하나의 그림으로 표현해서 모든 과정을 한 눈에 정리해보도록 하자.

여기까지 attention heads에 대해서 설명해 보았는데요, 이제 다시 우리의 예제 문장인 multi-head attention 과 함께 보도록 하자. 그중에서도 특히 "그것"이란 단어를 encode 할 때 여러 개의 attention이 각각 어디에 집중하는지를 보도록 하자.

우리가 "그것"이란 단어를 encode 할 때, 주황생의 attention head는 "그 동물"에 가장 집중하고 있는 반면 초록색의 head는 "피곤"이라는 단어에 집중을 하고 있다. 모델은 이 두개의 attention head를 이용하여 "동물"과 "피곤" 두 단어 모두에 대한 representation을 "그것"의 representation에 포함 할 수 있다.

그러나 이 모든 attention head들을 하나의 그림으로 표현하면, 이제 attention의 의미는 해석하기가 어려워진다.

Positional Encoding 을 이용해서 시퀀스의 순서 나타내기

우리가 이때까지 설명해온 Transformer 모델에서 한가지 부족한 부분은 이 모델이 입력 문장에서 단어들의 순서에 대해서 고려하지 있지 않다는 점이다.

이것을 추가하기 위해서, Transformer 모델은 각각의 입력 embedding에 "positional encoding"이라고 불리는 하나의 벡터를 추가한다. 이 벡터들은 모델이 학습하는 특정한 패턴을 따르는데, 이러한 패턴은 모델이 각 단어의 위치와 시퀀스 내의 다른 단어 간의 위치 차이에 대한 정보를 알 수 있게 해준다. 이 벡터들을 추가하기로 한 배경에는 이 값들을 단어들의 embedding에 추가하는 것이 query/key/value 벡터들로 나중에 투영되었을 때 단어들 간의 거리를 늘릴 수 있다는 점이 있다.

모델에게 단어의 순서에 대한 정보를 주기 위하여, 위치 별로 특정한 패턴을 따르는 positional encoding 벡터들을 추가한다.

만약 embedding의 사이즈가 4라고 가정한다면, 실제로 각 위치에 따른 positional encoding은 아래와 같은 것이다.

위는 크기가 4인 embedding의 positional encoding에 대한 실제 예시이다.

실제로는 이 패턴이 어떻게 될까?

다음 그림을 보자. 그림에서 각 행은 하나의 벡터에 대한 positional encoding에 해당한다. 그러므로 첫번째 행은 우리가 입력 문장의 첫 번째 단어의 embedding 벡터에 더할 positional encoding 벡터이다. 각 행은 사이즈 512인 즉 512개의 셀을 가진 벡터이며 각 셀의 값은 1과 -1 사이를 가진다. 다음 그림에서 이 셀들의 값들에 대해 색깔을 다르게 나타내어 positional encoding 벡터들이 가지는 패턴을 볼 수 있도록 시각화했다.

20개의 단어와 그의 크기 512인 embedding에 대한 positional encoding의 실제 예시이다. 그림에서 볼 수 있듯이 이 벡터들은 중간 부분이 반으로 나뉘어져있다. 그 이유는 바로 왼쪽 반은 (크기 256) sine 함수에 의해서 생성되었고, 나머지 오른쪽 반은 또 다른 함수인 cosine 함수에 의해 생성되었기 때문이다. 그 후 이 두 값들은 연결되어 하나의 positional encoding 벡터를 이루고 있다.

이 positional encoding에 대한 식은 논문의 section 3.5에 설명되어 있다. 실제로 이 벡터들을 생성하는 부분의 코드인 [get_timing_signal_1d()]https://github.com/tensorflow/tensor2tensor/blob/23bd23b9830059fbc349381b70d9429b5c40a139/tensor2tensor/layers/common_attention.py를 참고해도 좋다. 이것은 사실 positional encoding에 대해서만 가능한 방법은 아니다. 하지만 이것은 본 적이 없는 길이의 시퀀스에 대해서도 positional encoding 을 생성할 수 있기 때문에 scalability에서 큰 이점을 가진다.(예를 들어, 이미 학습된 모델이 자신의 학습 데이터보다도 더 긴 문장에 대해서 번역을 해야 할 때에도 현재의 sine과 cosine으로 이루어진 식은 positional encoding을 생성해낼 수 있다.)

The Residuals

encoder를 넘어가기 전에 그의 구조에서 한가지 더 언급하고 넘어가야 하는 사항은, 각 encoder 내의 sub-layer가 residual connection 으로 연결되어 있으며, 그 후에는 [layer-normalization]https://arxiv.org/abs/1607.06450 과정을 거친다는 것이다.

이 벡터들과 layer-normalization 과정을 시각화해보면 다음과 같다.

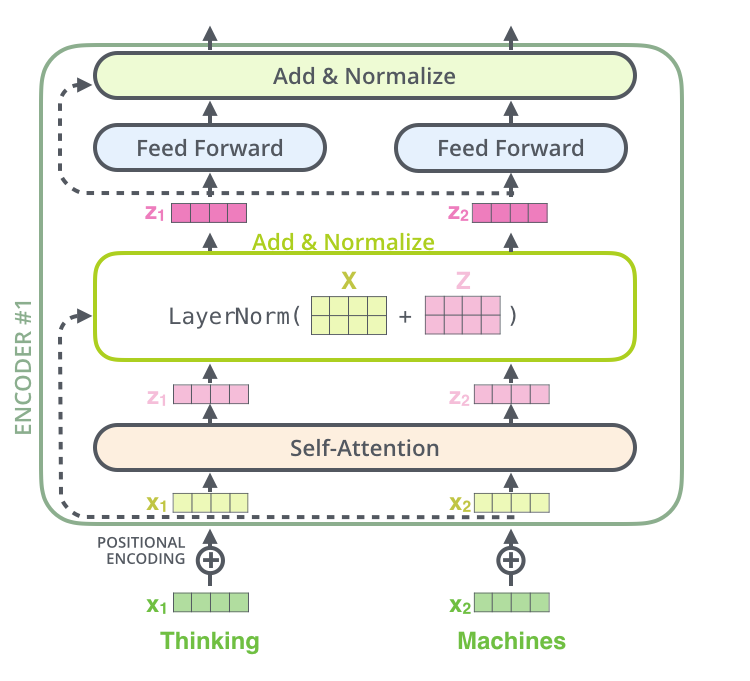
이것은 decoder 내에 있는 sub-layer 들에도 똑같이 적용되어 있다. 만약 우리가 2개의 encoder과 decoder으로 이루어진 단순한 형태의 Transformer 를 생각해본다면 다음과 같은 모양일 것이다.

The Decoder Side

이때까지 encoder 쪽의 대부분의 개념들에 대해서 얘기했기 때문에, 우리는 사실 decoder의 각 부분이 어떻게 작동하는지에 대해서는 이미 알고 있다고 봐도 된다. 하지만, 이제 우리는 이 부분들이 모여서 어떻게 같이 작동하는지에 대해서 보아야 한다.

encoder가 먼저 입력 시퀀스를 처리하기 시작한다. 그다음 가장 윗단의 encoder의 출력은 attention 벡터들인 K와 V로 변형된다. 이 벡터들을 이제 각 decoder의 "encoder-decoder attention" layer에서 decoder가 입력 시퀀스에서 적절한 장소에 집중할 수 있도록 도와준다.

이 encoding 단계가 끝나면 이제 decoding 단계가 시작된다. decoding 단계의 각 스텝은 출력 시퀀스의 한 element를 출력한다. (현재 기계 번역의 경우에는 영어 번역 단어이다)

decoding step은 decoder가 출력을 완료했다는 special 기호인 를 출력할 때까지 반복된다. 각 스텝마다의 출력된 단어는 다음 스텝의 가장 밑단의 decoder에 들어가고 encoder와 마찬가지로 여러개의 decoder를 거쳐 올라간다. encoder의 입력에 했던 것과 동일하게 embed를 한 후 positional encoding을 추가하여 decoder에게 각 단어의 위치 정보를 더해준다.

decoder 내애 있는 self-attention layer 들은 encoder와는 조금 다르게 작동한다.

decoder 에서의 self-attention layer은 output sequence 내에서 현재 위치의 이전 위치들에 대해서만 attend 할 수 있다. 이것은 self-attention 계산 과정에서 softmax를 취하기 전에 현재 스텝 이후의 위치들에 대해서 masking(즉 그에 대해서 -inf로 치환하는것)을 해줌으로써 가능해진다.

"Encoder-Decoder Alttention" layer은 multi-head self-attention 과 한 가지를 제외하고는 똑같은 방법으로 작동한다. 그 한가지 차이점은 Query 행렬들을 그 밑의 layer에서 가져오고 Key와 Value 행렬들을 encoder의 출력에서 가져온다는 점이다.

마지막 Linear Layer와 Softmax Layer

여러 개의 decoder를 거치고 난 후에는 소수로 이루어진 벡터 하나가 남게 된다. 어떻게 이 하나의 벡터를 단어로 바꿀 수 있을까? 이것이 바로 마지막에 있는 Linear layer와 Softmax layer가 하는 일이다.

Linear layer는 fully-connected 신경망으로 decoder가 마지막으로 출력한 벡터를 그보다 훨 씬 더 큰 사이즈의 벡터인 logits 벡터로 투영시킨다.

우리의 모델이 training 데이터에서 총 10,000개의 영어 단어를 학습하였다고 가정하자 (이를 우리는 모델의 "output vocabulary"라고 부른다). 그렇다면 이 경우에 logits vector의 크기는 10,000이 될 것이다 - 벡터의 각 셀은 그에 대응하는 각 단어에 대한 점수가 된다. 이렇게 되면 우리는 Linear layer의 결과로서 나오는 출력에 대해서 해석을 할 수 있게 된다.

그 다음에 나오는 softmax layer는 이 점수들을 확률로 변환해주는 역할을 한다. 셀들의 변환된 확률 값들은 모두 양수 값을 가지며 다 더하게 되면 1이 된다. 가장 높은 확률 값을 가지는 셀에 해당하는 단어가 해당 스텝의 최종 결과물로서 출력되게 된다.

위의 그림에 나타나 있는 것과 같이 decoder에서 나온 출력은 Linear layer 와 softmax layer를 통과하여 최종 출력 단어로 변환된다.

학습 과정 다시 보기

이제 학습된 Transformer의 전체 forward-pass 과정에 대해서 알아 보았으므로, 이제 모델을 학습하는 방법에 대해서 알아보자.

학습 과정 동안, 학습이 되지 않은 모델은 정확히 같은 forward pass 과정을 거칠 것이다. 그러나 우리는 이것을 label된 학습 데이터 셋에 대해 학습시키는 중이므로 우리는 모델의 결과를 실제 label 된 정답과 비교할 수 있다.

이 학습 과정을 시각화하기 위해, 우리의 output vocabulary 가 6개의 단어만 (("a","am","i","thanks","student",and "")) 포함하고 있다고 가정하자.

모델의 output vocabulary는 학습을 시작하기 전인 preprocessing 단계에서 완성된다.

이 output vocabulary를 정의한 후에는, 우리는 이 vocabulary의 크기만 한 벡터를 이용하여 각 단어를 표현할 수 있다. 이것은 one-hot encoding이라고 불린다. 그러므로 우리의 예제에서는 단어 "am"을 다음과 같은 벡터로 나타낼 수 있다.

이제 모델의 loss function에 대해서 얘기해보자. 이것은 학습 과정에서 최적화함으로써 모델을 정확하게 학습시킬 수 있게 해주는 값이다.

Loss Function

우리가 모델을 학습하는 상황에서 가장 첫 번째 단계라고 가정하자. 그리고 우리는 학습을 위해 "merci"라는 불어를 "thanks"로 번역하는 간단한 예시를 생각해보자.

이말은 즉, 우리가 원하는 모델의 출력은 "thanks" 라는 단어를 가리키는 확률 벡터라는 것이다. 하지만 우리의 모델은 아직 학습이 되지 않았기 때문에, 아직 모델의 출력이 그렇게 나올 확률은 매우 작다.

학습이 시작될 때 모델의 parameter들 즉 weight들은 랜덤으로 값을 부여하기 때문에, 아직 학습이 되지 않은 모델은 그저 각 cell(word)에 대해서 임의의 값을 출력한다. 이 출력된 임의의 값을 가지는 벡터와 데이터 내의 실제 출력값을 비교하여, 그 차이에 backpropagation 알고리즘을 이용해 현재 모델의 weight들을 조절해 원하는 출력값에 더 가까운 출력이 나오도록 만든다.

그렇다면 두 화귤ㄹ 벡터를 어떻게 비교할 수 있을까? 간단하다. 하나의 벡터에서 다른 하나의 벡터를 빼버린다. [Cross-entropy]https://colah.github.io/posts/2015-09-Visual-Information/ 와[Kullback-Leibler-divergence]https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained를 보면 이 과정에 대해 더 자세한 정보를 얻을 수 있다.

하지만 여기서 하나 주의할 것은 우리가 고려하고 있는 예제가 지나치게 단순화된 경우라는 것이다. 조금 더 현실적인 예제에서는 한 단어보다는 긴 문장을 이용할 것이다. 예를 들면 입력은 불어 문장 "je suis étudiant"이며 바라는 출력은 "i am a student"일 것이다. 이말인 즉, 우리가 우리의 모델이 출력할 확률 분포에 대해서 바라는 것은 다음과 같다.

• 각 단어에 대한 확률 분포는 output vocabulary 크기를 가지는 벡터에 의해서 나타내진다.(우리의 간단한 예제에서는 6이지만 실제 실험에서는 3,000 혹은 10,000과 같은 숫자일 것이다)
• decoder가 첫 번째로 출력하는 확률 분포는 "i"라는 단어와 연관이 있는 cell에 가장 높은 확률을 줘야 한다.
• 두 번째로 출력하는 확률 분포는 "am"라는 단어와 연관이 있는 cell에 가장 높은 확률을 줘야 한다.
• 이와 동일하게 마지막 ''를 나타내는 다섯 번째 출력까지 이 과정은 반복된다.

위의 그림은 학습에서 목표로 하는 확률 분포를 나타낸 것이다.

모델을 큰 사이즈의 데이터 셋에서 충분히 학습을 시키고 나면, 그 결과로 생성되는 확률 분포들은 다음과 같아질 것이다.

학습 과정 후에, 바라건대, 모델은 정확한 번역을 출력할 것이다. 물론, 우리가 예제로 쓴 문장이 학습 데이터로 써졌다는 보장은 없다. 그리고 한가지 여기서 특이한 점은 학습의 목표로 하는 벡터들과는 달리, 모델의 출력값은 비록 다른 단어들이 최종 출력이 될 가능성이 거의 없다 해도 모든 단어가 0보다는 조금씩 더 큰 확률을 가진다는 점이다. 이것은 학습 과정을 도와주는 softmax layer의 매우 유용한 성질이다.

모델은 한 타임 스텝 당 하나의 벡터를 출력하기 때문에 우리는 모델이 가장 높은 확률을 가지는 하나의 단어만 저장하고 나머지는 버린다고 생각하기 쉽다. 그러나 그것은 greedy decoding이라고 부르는 한가지 방법일 뿐이며 다른 방법들도 존재한다. 예를 들어 가장 확률이 높은 두 개의 단어를 저장할 수 있다.(위의 예시에서는 'i' 와 'student') 그렇다면 우리는 모델을 두번 돌리게 된다. 한번은 첫 번째 출력이 'i'라고 가정하고 다른 한 번은 'student'.라고 가정하고 두 번째 출력을 생성해보는 것이다. 이렇게 나온 결과에서 첫 번째와 두 번째 출력 단어를 동시에 고려했을 때 더 낮은 에러를 보이는 결과의 첫 번째 단어가 실제 출력으로 선택된다.

이과정을 두 번째, 세 번째, 그리고 마지막 타임 스텝까지 반복해 나간다. 이렇게 출력을 결정하는 방법을 우리는 "beam search"라고 부르며, 고려하는 단어의 수를 beam size, 고려하는 미래 출력 개수를 top_beams라고 부른다. 우리의 예제에서는 두 개의 단어를 저장 했으므로 beam size가 2이며, 첫 번째 출력을 위해 두 번째 스텝의 출력까지 고려했으므로 top_beams 또한 2인 beam search를 한 것이다. 이 beam size와 top_beams는 모두 우리가 학습전에 미리 정하고 실험해볼 수 있는 hyperparameter들 이다.

참고자료

위 참고자료를 필사한 내용입니다

Convolution

Image Data

• 먼저 이미지를 정형 데이터화 하는 방법을 생각해보자. 정형 데이터화 라는 말은 컴퓨터로 식별가능한 형태로 데이터를 변환하는 것을 의미한다. 예를 들어, 남자/여자라는 내요잉 있으면, 남자를 0 여자를 1로 하겠다와 같은 약속을 정형화한다고 한다. 임지ㅣ는 픽셀 단위로 구성이 되어 있고, 각 픽셀은 RGB 값으로 구성되어 있다. 즉 아주 자즉안 색이 담긴 네모 상자가 여러개가 모여 이미지가 되며, 색은 R(빨강), G(초록), B(파랑)의 강도의 합으로 표현할 수 있다. 이미지를 정형 데이터화 하는 것 방법 중 하나는 흑백 이미지의 경우 '가로x세로'에 흑색의 강도가 들어간 배열로, 컬러이미지의 경우 '가로x세로x3'의 배열로 나타낼 수 있으며 마지막 3에는 각각 R,G,B의 강도의 값으로 구성할 수 있다.

Convolutional Layer (합성곱 층)

Convolutional Layer가 왜 필요한가?

• 다음과 같은 3x3 이미지를 고려해보자. 우리가 일반 딥러닝 구조로 이미지를 분석한다는 것은 3x3 배열을 오른쪽 처럼 펼쳐서(Flattening)하여 각 픽셀에 가중치를 곱하여 은닉층으로 연산 결과를 전달하는 것과 같다. 이미지의 특성상 각 픽셀 간에 밀접한 상관 관계를 가지고 있을텐데, flattening해서 분석하면 데이터의 공간적 구조를 무시한다는 것을 쉽게 알 수 있다. 이미지 데이터의 공간적인 특성을 유지하는 것이 convolutional layer의 등장에 큰 동기가 되었다.

Convolution (합성곱) 이란?

Convolution은 두 함수 $(f,g)$를 이용해서 한 함수$(f)$의 모양이 나머지 함수 (g)에 의해 모양이 수정된 제 3의 함수 $(f * g)$를 생성해주는 연산자로 통계, 컴퓨터 비전, 자연어 처리, 이미지 처리, 신호 처리 등 다양한 분야에서 이용되는 방법이다. Convolution의 정의는 다음과 같다.

$\left(f*g\right)(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau$

Convolution의 정의를 그대로 이해하면 y축 기준 좌우가 반전이 된 함수 $g$를 우측으로 t만큼 이동한 함수$g(t-\tau)$와 $f(\tau)$를 곱해진 함수의 적분이다. 다움 두 함수 $f,g$를 고려해보자.

함수 $f,g$는 $f(t)=I\left(t\in[0,1]\right)$,$g(t)=tI\left(t\in[0,1]\right)$입니다. 먼저 $t = 3$인 경우를 생각해보자.

빨간선 $f$는 고정된 것과 파란선 g를 y축 대칭시킨뒤 우측으로 3만큼 이동한 것을 볼 수있는데, 이 때 두 하숨를 곱한 것이 적분 대상이 되며 초록띠와 대응된다. 초록띠와 x축으로 둘러 쌓인 면적이 0이므로 $t=0$의 convolution은 0이 된다.
$t = 0.5$ 일때는 다음과 같다.

초록띠와 x축으로 둘러 쌓인 면적은 0.25로 $t = 0.5$에서 convolution 결과이다. t를 $-\infty$ 부터 $\infty$ 까지 순차적으로 살펴보면 다음과 같다.

최상단의 그림은 함수 g가 이동하면서 연산의 적분 대상함수의 모습을 가운데는 convolution 결과가 순차적으로 생성되는 과정을, 마지막은 $f * g$의 결과이다.

추가적으로 Cross-correlation이 있다. Cross-correlation은

$(f*g)(t)\int_{-\infty}^{\infty}f(\tau)g(t+\tau)$

이다. g에서 y축 반전을 거치지 않는 것이 convolution과의 차이이다. 비교해서 살펴보면 아래와 같다.

Convolutional Layer의 연산법은 정확하게 cross-correlation이다. 하지만 CNN에서는 가중치를 학습하기 때문에 convolution과 cross-correlation을 정확히 구분 할 필요가 없다.

Convolutional Layer(합성곱 층)

Convolutional layer는 아래 그림과 같이 빨간 상자를 sliding window 방식으로 가중치와 입력값을 곱한 값에 활성함수를 취하여 은닉층으로 넘겨준다.

Convolution layer는 사람이 실제로 보는 것을 우측의 파란 3x3 픽셀 이라고 했을떄, 전체를 인시갛는 것이 아니라, 일부분을 빨간색 상자로 투영하고 그를 우측의 주황색 수용 영역에 연결되어 복합적으로 해석하는 것을 모방한 것이다.

Convolutional Latyer 계산 방법 개요

위 그림의 좌측은 흑백 이미지의 픽셀 값이고, 우측은 좌측의 이미지를 투영하여 convolution(합성곱 연산)을 하는것으로 필터(filter) 혹은 커널 (kernel) 또는 윈도우 (window)라고 부른다.

딥러닝 프레임워크 관점에서 말하면 픽셀 값은 입력 값(input)이 되고, 필터 값은 가중치(weight)가 된다.

이미지 좌상단에 이미지와 필터를 포개놓고 대응되는 숫자끼리 곱한 뒤, 모든 숫자를 더해주면 된다.
이어서 필터를 sliding window 방식으로 이동해가며 합성곱 연산을 수행하면 된다.

합성곱 연산의 결과를 특성(feature) 라고 부른다. 위 예제 기준으로 만약 이미지를 Flattening한다면 16개 가중치를 학습해야 될 것이다. 보는것처럼 convolutional layer를 도입하여 학습할 가중치가 4개로 줄었고 컴퓨터 연산의 수를 획기적으로 감소시켰다.

가중치에는 편의(bias)를 더해준것처럼 Convolutional Later에서도 편향을 더해주기도 한다.

Stride (스트라이드)

필터를 입력데이터나 특성에 적용할 때 움직이는 간격을 스트라이드(Stride) 라고 한다.

Padding (패딩)

패딩은 반복적으로 합성곱 연산을 적용했을 때 특성의 행렬의 크기가 작아짐을 방지하는 것과 이미지의 모서리 부분의 정보손실을 줄이고자 이미지 주변을 0으로 채워넣는 방법이다.

1d convolution

1x1 Convolution 에는 크게 세가지 장점이 있다.

1. Channel 수 조절

Convolution Layer를 사요앟여 Custom Model을 구성할 경우, Channel 수는 하이퍼파라미터이기 때문에 우리가 직접 결정해주어야 한다. 대부분은 논문을 참조하지만 그렇지 않은 경우 특성에 맞게 결정한다.

이 부분에서 1x1 Conv의 장점인 Channel 수를 우리가 원하는 만큼 결정 할 수 있다. 하지만 Convolution 연산에서는 특히 충분히 큰 크기의 channel 수를 사용하고자 할 때 문제가 발생한다. 왜냐하면 그만큼 파라미터 수가 급격히 증가하기 때문이다. 하지만 1x1 Convolution을 사용하면 효율저긍로 모델을 구성함과 동시에 만족할만한 성능을 얻을 수 있다.

2. 계산량 감소

여기서 파라미터 수는 주로 결과값 크기를 의미한다. 밑 그림에서 (28*28)을 제거해야 진정한 의미의 파라미터 수라고 말할 수 있다. 하지만 편의를 위해 파라미터 수라고 언급하도록 하겠다.

위 그림처럼 Channel 수 조절은 직접저긍로 계산량 감소로 이어지게 되어 네트워크를 구성할 때 좀 더 깊게 구성할 수 있도록 도움을 준다. 특히 위처럼 Channel 수를 줄였다가 다시 늘이는 부분을 Bottle neck 구조라고 표현하기도 한다. 파라미터 수가 많으면 아무리 보유하고 있는 GPU나 RAM이 좋아도 감당하기 힘드니 충분히 고려해볼만한 방법이다.

3. 비선형성

GoogLeNet을 포함하여 구글팀의 수많은 고민이 포함되어 적용된 Inception 계통의 다양한 model version을 공부하면, 많은 수의 1x1 Conv를 사용했다는 것을 알 수있다. 이때 ReLU를 지속적으로 사용하여 모델 비선형성을 증가시켜 준다. ReLU 사용 목적 중 하나는 모델의 비선형성을 더해주기 위함도 있다. 비선형성이 증가한다는 것은 그만큼 복잡한 패턴을 좀 더 잘 인식할 수 있게 된다는 의미와 비슷하다.

AlexNet

AlexNet은 일부가 Max-pooling layer가 적용된 5개의 convolution layer와 3개의 fully-connected layer로 이루어져 있다.

AlexNet의 구조에 적용된 특징

1. ReLU Nonlinearity
   활성화 함수로 ReLU 를 적용시켰다.
   4층의 CNN으로 CIFAR-10을 학습시켰을 때 ReLU가 tanh보다 6배 빠르다고 한다.
2. Traingng on Multiple GPUs
   network를 2개의 GPU로 나누어 학습시켰다. 120만개의 data를 학습시키기 위한 network은 하나의 GPU로 부족하다고 설명했다. 2개의 GPU로 나누어 학습시키니 top-1 error와 top-5 error가 1.7% 1.2%씩 감소되고 학습속도가 빨라졌다고 한다.
3. Local Response Nrmalization(LRN)
   LRN은 generalization을 목적으로한다. 논문에서는 LRN을 측면 억제(later inhibition)의 형태로 구현한다고 나와있다. AlexNet 이후 현대의 CNN에서는 LRN 대신 batch normalization 기법이 쓰인다.
4. Overlapping Pooling
   Overlapping pooling을 통해서 overfit을 방지하고 top-1와 top-5 error를 각각 0.4% 0.3% 낮추었다고 한다.
5. data augmentation
6. Dropout

VGGNet

ILSVRC 2012에서 우승한 AlexNet(8 layer) 과 비교하여 VGG(16-19 layer)는 2배가량 깊어졌다.
VGGNet은 항상 이웃픽셀을 포함할 수 있는 가장 작은 3x3 필터만 사용한다.
이렇게 작은 필터를 유지해 주고 주기적으로 Pooling을 수행하며 전체 네트워크를 구성한다.

GoogLeNet

이 모델의 주요 특징은 연산을 하는데 소모하는 자원의 사용 효율이 개선되었다는 것이다. 즉, 정교한 설계 덕에 네트워크의 depth와 width를 늘려도 연산량이 증가하지 않고 유지된다는 뜻이다. 이때 Google팀에서는 성능을 최적화하기 위해서 Hebbian principle과 multi-scale processing을 적용하였고, 이 구조를 GoogLeNet이라 부른다고 한다. GoogLeNet은 22개의 layer를 가지며, 코드네임은 Inception이다.

GoogLeNet에 영향을 많이 끼친 논문중 Network in Network는 신경망의 표현력을 높이기 위해 제안된 접근법이다. 이 방법은 1x1 Convolutional layer가 추가되며, ReLU activation이 뒤따른다. 이 때 1x1 Convolutional layer는 두 가지 목적으로 사용된다.

병목현상을 제거하기 위한 차원 축소와 네트워크 크기 제한이다.

ResNet

딥러닝에서 neural networks가 깊어질수록 성능은 더 좋지만 train이 어렵다는 것은 알려진 사실이다. 그래서 이 논문에서는 residual(잔차)를 이용한 잔차학습(residual learning framework)를 이용해서 깊은 신경망에서도 training이 쉽게 이뤄질 수 있다는 것을 보이고 방법론으로 제시했다.

DenseNet

DenseNet은 ResNet과 Pre-Activation ResNet보다 적은 파라미터 수로 더 높은 성능을 가진 모델이다. DensNet은 모든 레이어의 피쳐맵을 연결한다. 이전 레이어의 피쳐맵을 그 이후의 모든 레이어의 피쳐맵에 연결한다 연결할 때는 ResNet과 다르게 덧셈이 아니라 concatenate(연결)을 수행한다. 따라서 연결할 때는 피쳐맵 크기가 동일해야 한다. 피쳐맵을 계속해서 연결하면 채널 수가 많아질 수 있기 때문에, 각 레이어의 피쳐맵은 채널 수는 굉장히 작은 값을 사용합니다.

이렇게 연결하면 어떤 장점이 있을까?

• 1. strong gradeint flow와 information flow를 갖는다. 이는 기울기 소실 문제를 완하하고 feature reuse 효과가 있다.
• 2. 파라미터수와 연산량이 적어진다.

참고자료

(https://yjjo.tistory.com/8)

(https://hwiyong.tistory.com/45)

(https://phil-baek.tistory.com/entry/3-GoogLeNet-Going-deeper-with-convolutions-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0)

(https://kangbk0120.github.io/articles/2018-01/inception-googlenet-review)

(https://codebaragi23.github.io/machine%20learning/3.-ResNet-paper-review/)

(https://deep-learning-study.tistory.com/528)

일반화(Generalization)

• 학습데이터와 Input data가 달라져도 출력에 대한 성능 차이가 나지 않게 하는 것을 일반화라고 한다. 즉 Generalzation Error 을 줄이는게 목표.

Bias and Variance

Booststrapping

• 데이터 내에서 반복적으로 샘플을 사용하는 resampling 방법 중 하나이다.

Optimization 종류 및 설명

Regularization

Early stopping

• 학습 횟수(=epoch 수) 가 많을수록 학습 데이터에 관한 오차는 작아지지만 이것이 오버피팅(over fitting)을 초래해서 모델의 일반화 성능이 떨어지게 된다.

이 문제를 해결하기 위해 사용되는 방법이 Early Stopping 으로 이전 epoch 때와 비교해서 오차가 증가했다면 학습을 중단한다 는 방법이다.

Data Augmentation

데이터의 수가 부족해 데이터를 부풀려내는 방법.

DMQA data augmentation 세미나 발표 영상

Noise robustness

Label smoothing

모델이 Ground Truth(GT)를 정확하게 예측하지 않아도 되게 만들어 주는 것이다.
모델이 정확하지 않은 학습 데이터셋에 치중되는 경향을 막아 calibration 및 regularization 효과를 가질 수 있다.

Dropout

기본 신경망의 구조는 왼쪽처럼 각 레이어가 노드로 연결되어 있다. 하지만 위의 그림에서도 쉽게 볼 수 있듯이, 모델이 깊어짐에 따라 선들이 매우 많아지게 됨을 확인할 수 있다. 즉 너무 열심히 학습하게 된다는 것이다.

이렇게 과적합이 되는걸 방지하기 위해 (Overfitting을 막기 위해) 인간처럼 기억을 잊을 수 있게 한 것이 Dropout 이다. 선택적으로 노드를 Drop 하는 것이다.

Batch normalization

참고자료 : (https://www.boostcourse.org/),(https://blog.naver.com/PostView.nhn?blogId=winddori2002&logNo=221850530979)

교차 검증 (Cross Validation)

교차검증의 필요성

• 교차검증을 하는 이유는 과적합을 피하면서 파라미터를 튜닝하고 일반적인 모델을 만들고 더 신뢰성 있는 모델 평가를 진행하기 위해서이다.

• 우리는 일반적으로 전체 데이터를 7:3으로 나누고 train set을 학습하여 test set으로 평가한다.
  이 경우 문제점은 우리가 학습한 모델이 제대로 학습되었는지, 또 모델을 학습하는 데에 있어서 train set에 과적합이 된건 아닌지 확인 할 수 없다.
  그래서 우리는 최종 평가 전에 모델을 학습하기 위해서 validation set을 지정한다.

• 위와 같이 데이터셋을 구성한다면 더 이상 train set으로만 학습하는 것이 아니라 validation set으로 평가하면서 하이퍼 파라미터를 튜닝하고 모델을 학습할 수 있다.
  하지만 여전히 생기는 문제점은 있다. 앞선 방법이 train set 에만 과적합되었다면 이번에는 validation set 에만 과적합 될 수 있다. 또한 모델을 평가하는데 있어서 특정 데이터셋에서만 성능이 잘 나와 test set 에서는 성능이 잘 나오지 않는 경우가 생길 수 있다.

• 이렇듯 과적합을 피하고자 validation set을 구성하더라도 하나의 validation set으로만 구성한다면 하나의 validation set만 잘 맞추는 파라미터를 튜닝하고 모델을 학습하게 될 수 있습니다. 그래서 하나의 검증이 아닌 여러번의 검증으로 일반적인 모델을 만들고 파라미터를 튜닝하기 위해서 교차검증이 등장합니다.

교차검증의 종류

K-Fold Cross Validation

• K-Fold CV는 가장 일반적이고 많이 사용되며 강력한 교차 검증 방법 중 하나이다. 말 그대로 k개의 fold를 구성하는데 즉 k개의 다른 데이터셋을 구성하고 모델을 각각 학습하는 방법이다.

• k-flod 에서 k 는 우리가 지정할 수 있다. 위의 그림에서는 k를 5로 지정하였고 전체 데이터를 임의로 1/5로 나누어 validation set을 한번씩 번걸아가면서 데이터셋을 구성하였다.

• 각 데이터를 학습하고 validation으로 평가를 한 다음 5개의 결과에 대해 평균을 내어 최종 성능을 구한다. 이러한 식으로 데이터를 구성한다면 우선 모델 평가부분에서 고정된 validation set이 아니기 때문에 신뢰성 있는 결과를 얻을 수 있다.

Stratified K-fold Cross Validation

• 층화 k-fold CV는 기존 k-fold CV와 비슷한 방법으로 수행되나 계층을 고려 하는 방법이다

• 기존 k-fold 방법을 사용한다면 데이터가 임의로 섞이면서 validation set에 특정 클래스가 과하게 분포될 수 있다. 예시로 전체 데이터 중 클래스 0이 80%, 1이 20% 라고 하자.

• 그렇다면 어떤 flod에서는 다음과 같이 클래스 비율이 상이하게 분포되어 원치 않는 결과를 도출할 수도 있다. 그래서 층화 k-fold CV는 전체 데이터의 클래스 비율을 고려하여 set을 구성한다.

• 일반적으로 클래스가 있는 분류 문제에서는 층화 k-fold CV를 활용하며 회귀 문제에서는 K-fold CV를 활용한다.

Leave One Out Cross Validation(LOOCV)

• LOOCV 방법은 하나의 데이터만 남기고 나머지 데이터로 학습을 하고 평가하는 방식이다. 만약 총 데이터가 N개라면 (N-1)개의 데이터로 학습하고 1개의 데이터로 평가한다. 총 N개의 데이터가 있기 때문에 하나씩 반복하면 N번 학습을 진행한다.

• K-Fold와 비교하자면 K가 데이터 개수 N인 경우 N-Fold CV라고 생각하면 된다. 이 방법은 데이터가 많으면 많을수록 굉장한 시간이 걸린다. 하지만 데이터를 하나씩 보면서 학습할 수 있기 때문에 bias는 광장히 작을 수도 있을 것이고, variance는 굉장히 클 수도 있다.

• LOOCV 방법은 일반적인 경우에는 추천하지 않으나 데이터의 개수가 많이 부족할 때는 유용한 결과를 도출할 수도 있는 방법이다.

Repeated Random Sub Sampling Validation

• 이 검증 기법은 임의로 validation set을 추출하여 평가하고 하이퍼파라미터를 튜닝할 수 있는 방법이다.

• 위의 빨간색 부분으로 처리된 부분이 임의로 선택된 validation set이다. 이런식으로 임의로 validation set을 지정하고 해당 set으로 평가하고 튜닝을 할 수 있다. 이 방법의 장점은 기존 k-fold와 다르게 데이터를 분할하는 것에 iteration이 종속되지 않는다는 것이다. 예를 들어 10-fold의 경우 10개의 validation set을 만든다면 10번의 itertation을 수행해야 하지만 이 기법은 사용자가 설정할 수 있다. **반면 임의로 선정되는 validation set으로써 validation set이 중복될 수도 있고 한번도 선택되지 않은 데이터가 있을 수도 있다.

Nested Cross Validation

• ested Cross Validation은 기존의 교차검증을 중첩한 방식이다.

• 이처럼 Nested CV는 Outer Loop와 Inner Loop로 구성되어 있다. outer loop에 구성된 각 폴드에는 train set과 test이 존재하는데 여기 존재하는 train set에서 inner loop가 작동한다. inner loop에서는 outer loop에 사용될 train set을 train subset과 validation set으로 분리하고 검증셋으로 평가하면서 파라미터를 튜닝한다. 그렇게 나온 성능의 평균이 가장 좋은 하이퍼파라미터가 나올 거고 해당 최적의 파라미터를 통해 fold1에서 test set으로 평가한다. 이러한 방식을 반복하는 방법이다.

• 결국 outer loop에서는 test set에 대한 평가를, inner loop에서는 각 폴드의 최적 파라미터를 튜닝하는 것이 목적이다.

• 굳이 이렇게 test set 또한 다양하게 나누어서 평가한 이유는 기존 방식처럼 랜덤하게 나눈 하나의 test set 또한 신뢰성이 없을 수 있다는 것이다. 그래서 다양하게 나눈 test set과 각각에 맞는 최적의 파라미터 튜닝한 모델을 통해 모델의 일반화를 추구한다.

DL Basic

어떤 것들이 훌륭한 Deep Learner를 만드는가?

1. 구현 실력(implementation skill)
2. 수학(math skills)
3. 최근 트렌드 연구(knowing a lot of recent papers)

딥러닝 구성요소의 핵심

1. 정보(Data) - 모델이 학습할 수 있는 데이터
2. 모델(Model) - 모델 데이터를 변환하는 방법
3. 손실(Loss) - 모델의 불량을 최소화하는 손실 함수
4. 알고리즘(algorithm) - 손실을 최소화 하기 위해 매개변수를 조정하는 알고리즘

Visualization

데이터의 종류

1. 데이터셋 ?
   • 정형 데이터
   • 시계열 데이터
   • 지리 데이터
   • 관계형(네트워크) 데이터
   • 계층적 데이터
   • 다양한 비정형 데이터

2. 데이터의 종류

- 수치형(numerical)
    - 연속형(continuous) : 길이, 무게, 온도 등
    - 이산형(discrete)   : 주사위 눈금, 사람 수 등 


- 범주형(categorical)
    - 명목형(nominal) : 혈액형, 종교 등
    - 순서형(ordinal) : 학년,별점,등급 등

궁금한 점?

Why Adam ?

RMS Propagation + Adagrad + Momentum + NAG = Adam

what is SimCLR?

https://rauleun.github.io/SimCLR

https://animilux.github.io/SimCLR/

아직 잘 모르겠음..

<참고자료>

https://velog.io/@yookyungkho

주간학습정리

1. 강의 복습 내용

https://junhyuk93.github.io/til/2021/08/02/Ai-BoostCamp-Day-1.html
https://junhyuk93.github.io/til/2021/08/03/Ai-BoostCamp-Day-2.html
https://junhyuk93.github.io/til/2021/08/04/Ai-BoostCamp-Day-3-(1).html
https://junhyuk93.github.io/til/2021/08/04/Ai-BoostCamp-Day-3-(2).html
https://junhyuk93.github.io/til/2021/08/05/Ai-BoostCamp-Day-4-python.html
https://junhyuk93.github.io/til/2021/08/05/Ai-BoostCamp-Day-4-CNN.html
https://junhyuk93.github.io/til/2021/08/06/Ai-BoostCamp-Day5-RNN.html

2. 과제 수행 과정 / 결과물 정리

• 과제 수행중 입력값에서 오류가 있다면 True 를 반환하는 함수를 제작했는데

import re
def validated_sentence(user_input):

    if len(re.findall(r'[0-9]',user_input)) >= 1:
        return False

    if len(re.findall(r'[_@#$%^&*()-+={};:\|`~]',user_input)) >= 1:
        return False

    if len(re.sub(r'[,.!?]', '', user_input)) == 0:
        return False

    if len(re.sub(r'[ ]', '', user_input)) == 0:
        return False

    if len("".join(user_input.split())) == 0:
        return False


    return True

이와 같이 작성했더니 예외로 빠지는 코드를 모두 잡을 수 없어서 오류가 발생했었다.

그래서 정규표현식에서 특수문자 검출방법과 예외처리 방식을 바꿔서 오류 수정후 문제를 해결할 수 있었다.

import re
def validated_sentence(user_input):
    clean_sentence = re.sub(r"[^.,!?a-zA-Z ]","",user_input)

    if (len(clean_sentence) != len(user_input)) or (re.sub(r"[.,!? ]","",user_input) == ""):
        result = False

    else:
        result = True

    return result

3. 피어세션 정리

회의록 참고

https://www.notion.so/level1-18-645fd2ecad4c451caf3fb86bd8f35d07

4. 학습 회고

프리코스에서 진행했던 파이썬 기초 강의들과 선형대수학 및 확률과 통계 기초강의, CNN과 RNN의 기초 강의를 들었다. 파이썬 모듈에 관한 부분은 사용할때나 다시 강의를 들을 때나 여전히 복잡하고 어려운 것 같다. 수학 강의와 과제에서 경사하강법 역시 항상 라이브러리를 이용하여 풀거나 line by line 로 해결했었는데 함수로 작성해서 사용하려 하니 복잡한 과정을 해결해야만 했었다.

확률과 통계 역시 볼때마다 익숙해지려면 약간의 시간이 필요했고, 궁금증 역시 생겼다. 이러한 과정에서 생긴 궁금증이나 질문들을 같은 팀 캠퍼분들에게 물어 해결했다. 처음 캠퍼분들과 피어세션에서 만났을 땐 아무래도 서로 어색하고 서먹했지만 이것 역시 시간이 해결해 줄 것이고, 지금은 서로 공부 내용에 대한 토의나 학습 과정에서 생길 수 있는 의문점 혹은 이 외에 다른 부분에 대한 의견들도 공유하며 소통해 나갈 수 있어서 정말 의지할 수 있는 팀이 될 것 같다.

RNN 이해하기

RNN

• 순환 신경망(Recurrent Neural Network, RNN) 은 인공 신경망의 한 종류로, 유닛간의 연결이 순환적 구조를 갖는 특징을 가지고 있다. 이러한 구조는 사변적 동적 특징을 모델링 할 수 있도록 신경망 내부에 상태를 저장할 수 있게 해주므로 순방향 신경망(feedforward neural network)과 달리 내부의 메모리를 이용해 시퀀스 형태의 입력을 처리할 수 있다. 따라서 순환 인공 신경망은 시변적 특징을 지니는 데이터를 처리하는데 적용할 수 있다.

기본적인 RNN 수식

• 시퀀스 데이터(sequence data) 란?
  각각의 데이터가 순서가 있는 데이터를 말하며, 시퀀스 원소들은 특정 순서를 가지므로 독립적이지 않다.
  대표적인 시퀀스 데이터로 시계열 데이터(시간의 흐름에 따라 기록된 데이터)와 텍스트 데이터(문맥이 존재), 주가 데이터 등 이 있다.

RNN 방식

1. 양방향 순환 신경망(Bi-directional RNN)

• 양방향 순환 신경망은 길이가 정해진 데이터 순열을 통해 어떤 값이 들어오기 전과 후의 정보를 모두 학습하는 방식의 알고리즘이다. 이를 위해 순열을 왼쪽에서 오른쪽으로 읽을 RNN 하나와, 오른쪽에서 왼쪽으로 읽을 RNN 하나를 필요로 한다. 이 둘의 출력값을 조합한 뒤 지도된 결과와 비교하여 학습하는 것이다. LSTM과 병용할 때 특히 좋은 성능을 낸다는 사실이 증명되었다.

2. LSTM(Long Short-Term Memory)

• LSTM은 기울기 소실 문제(vanishing gradient problem)를 해결하기 위해 고안된 딥 러닝 시스템이다. LSTM은 망각 게이트(forget gate)라 부르는 게이트를 추가적으로 가진다. 이 게이트를 통해 역전파시 기울기값이 급격하게 사라지거나 증가하는 문제를 방지할 수 있다. 이로써 기존의 RNN은 먼 과거의 일로부터 학습하는 것이 산술적으로 거의 불가능했지만, LSTM은 수백만 단위 시간 전의 사건으로부터도 학습할 수 있음으로서 고주파 신호뿐 아니라 저주파 신호까지도 다룰 수 있게 되었다.

3. GRU(Gated Recurrent Units, 게이트된 순환 유닛)

• GRU는 2014년에 처음으로 발명된 구조이고 출력게이트가 존재하지 않으므로, LSTM에 비해 더 적은 수의 매개변수를 가짐에도 불구하고 다성음악 학습이나 음성 인식 분야에서 LSTM과 유사한 성능을 가진다.

LSTM과 GRU의 차이점

• 망각게이트(forget gate)의 유무

  망각게이트(forget gate) : 과거 정보를 버릴지 말지 결정하는 과정. 즉, 망각게이트는 현재 입력과 이전 출력을 고려해서 cell state의 어떤 값을 버릴지 결정하는 역할.

참고자료

https://ko.wikipedia.org/
https://excelsior-cjh.tistory.com/154
http://colah.github.io/posts/2015-09-NN-Types-FP/
https://wegonnamakeit.tistory.com/7

Python 강의 공부

list comprehension

• 장점 : 일반적으로 for + append 보다 속도가 빠름.

# 일반적인 for 문

result_1 = []
for i in range(10):
    result.appen(i)


# cmprehension

result_2 = [i for i in range(10)]

result_3 = [i for i in range(10) if i % 2 == 0 if i <= 6] # 이와 같이 조건 부여도 가능

• 리스트 출력할때 pprint 로 깔끔하게 출력

Lambda

# 일반적인 함수
def f(x,y):
    return x + y

print(f(1,4))

# lambda 문

(lambda x, y : x + y)(1,4)

• 익숙하지 않아 거리감이 있었는데 연습해보려고 다시 써보니 역시 왜 쓰는지 잘 모르겠음.

return 과 yield 의 차이

return 을 이용해서 랜덤한 수를 반환해주는 함수.

임의의 수를 생성하고 이를 10회 반복하려 return 하도록 구성.

이렇게 작성할 시, return이 호출되면 반복을 멈추고, 수를 반환하기 때문에 hello 가 출력되지 않음.

그리고 이 때 만들었던 임의의 수는 메모리에서 할당 해제되어 다시 호출할 수 없음.

반면 같은 기능을 하는 함수를 return 대신 yield를 사용해서 작성.

yield가 호출되면 함수는 그 시점에서 일시 정지됨.

그리고 그 시점에 함수 안에 선언되어 있는 변수들을 기억하고 next()를 통해 실행되면

yield 바로 다음 라인부터 다시 실행을 이어나감.

즉 yield 를 호출하면 원하는 값을 리턴하며, 실행 흐름을 일시 정지하여 함수를 재활용할 수 있는 상태로 만듬.

(참고자료:https://yeomko.tistory.com/11)

CNN 이해하기

• 합성곱 신경망 (Convolutional neural network, CNN)은 시각적 영상을 분석하는 데 사용되는 다층의 피드-포워드적인 인공신경망의 한 종류이다. 공유 가중치 구조와 변환 불변성 특성에 기초하여 변이 불변 또는 공간 불변 인공 신경망(SIANN)으로도 알려져 있다. Convolution 연산은 커널(kernel)을 입력 벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다. CNN 은 크게 합성곱 계층(Convolution layer)과 풀링 계층(Poolding layer)으로 구성된다.

• 합성곱 계층(Convolution layer)

  이미지와 같은 3차원 데이터를 입력 받으면 다음 계층에도 3차원 데이터로 전달한다. CNN에서 합성곱 계층의 입출력 데이터는 다차원이기에 이것을 특징 맵(Feature Map)이라고 한다. 입력 데이터를 입력 특징 맵(Input Feature), 출력데이터를 출력 특징 맵(Output Feature Map) 이라고 한다.

• 패딩(Padding)

  합성곱 연산을 수행하기 전에 입력 데이터 주변은 특정 값(0,1 등)으로 채우기도 하는데, 이를 패딩이라 하며 합성곱 연산에서 자주 이용되는 기법이다. 폭 1짜리 패딩이면 데이터 사방 1픽셀을 특정 값으로 채우는 것을 말한다.

패딩을 적용하는 이유는 출력의 크기를 조절하기 위함이다. 패딩 없이 입력 데이터에 필터를 씌워 합성곱 연산을 수행하면 출력 데이터는 입력 데이터에 비해 무조건 작아지게 되어있다. 합성곱 연산을 반복하면 어느 시점에서는 출력 크기가 1이 되고, 더이상 합성곱 연산을 수행할 수 없게 된다. 이러한 사태를 방지하기 위해 패딩을 사용하는 것이다. 패딩을 사용하면 출력 데이터의 크기를 입력 데이터의 크기와 동일하게 설정할 수 있다.

다양한 차원에서의 Convolution

1D-conv

2D-conv

3D-conv

i,j,k가 바뀌어도 커널 $f$ 의 값은 바뀌지 않음.

Convolution 연산의 역전파

• 오류 역전파 알고리즘(Backpropagation Algorithm)은 정방(Feedforward) 연산 이후, 에러예측값과 실제값의 오차를 후방(Backward)으로 다시 보내 줌으로써, 많은 노드를 가진 MLP라도 최적의 Weight와 Bias를 학습할 수 있도록 한다.

• Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.

(참고자료)

https://zsunn.tistory.com/entry/AI-CNN%EA%B3%BC-RNN%EC%9D%98-%EC%9D%B4%ED%95%B4

https://kolikim.tistory.com/53?category=733477

https://ko.wikipedia.org/wiki

http://solarisailab.com/archives/1206